Exercie 1er s
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
ore98
- Membre Naturel
- Messages: 11
- Enregistré le: 22 Mar 2015, 10:37
-
 par ore98 » 22 Mar 2015, 10:56
par ore98 » 22 Mar 2015, 10:56
Soit Un la suite definie pour tout entier naturel non nul de n par : Un=1^2+2^2+...+n^2
1) Donner l'expression de Un+1 en fonction de Un et le premier terme U1 de la suite
2) a) on considère maintenant la suite Wn definie par : Wn=(n×(n+1)(2n+1))÷6
Determiner W1 et Wn+1-Wn, puis l'expression de Wn+1 en fonction de Wn
b) en déduire que 1^2+2^2+...+n^2= (n×(n+1)(2n+1))÷6
-
ore98
- Membre Naturel
- Messages: 11
- Enregistré le: 22 Mar 2015, 10:37
-
 par ore98 » 22 Mar 2015, 11:00
par ore98 » 22 Mar 2015, 11:00
Je bloc surtout sur la question 1 car je ne sais pas donner l'expression de Un+1 en fonction de Un
Je vous remercie d'avance
-
mathelot
 par mathelot » 22 Mar 2015, 11:02
par mathelot » 22 Mar 2015, 11:02
-
ore98
- Membre Naturel
- Messages: 11
- Enregistré le: 22 Mar 2015, 10:37
-
 par ore98 » 22 Mar 2015, 11:05
par ore98 » 22 Mar 2015, 11:05
Merci de m'avoir répondu mais je ne vois pas pourquoi tu fait ça
-
mathelot
 par mathelot » 22 Mar 2015, 11:18
par mathelot » 22 Mar 2015, 11:18
ore98 a écrit:Merci de m'avoir répondu mais je ne vois pas pourquoi tu fait ça
pour que tu puisses répondre à la question (1) :doh:
écrire

fonction de

, c'est déterminer ce qui est invariant dans la formule
(l'exposant 2)
et ce qui ne l'est pas (le nombre de termes de la somme qui augmente de 1).
à la 2.b) il y aura une récurrence à faire sur l'égalité

-
ore98
- Membre Naturel
- Messages: 11
- Enregistré le: 22 Mar 2015, 10:37
-
 par ore98 » 22 Mar 2015, 11:25
par ore98 » 22 Mar 2015, 11:25
ore98 a écrit:Merci de m'avoir répondu mais je ne vois pas pourquoi tu fait ça
C bon j'ai compris pourquoi j'en est donc déduit que Un+1=Un+(n+1)^2
Et je ne trouve pas pour l'expression de Wn+1 en fonction de Wn
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 22 Mar 2015, 11:40
par Shew » 22 Mar 2015, 11:40
ore98 a écrit:C bon j'ai compris pourquoi j'en est donc déduit que Un+1=Un+(n+1)^2
Et je ne trouve pas pour l'expression de Wn+1 en fonction de Wn
On a
(2n + 1)}{6})
on traite donc n en fonction de l'indice de W :
*((n + 1) + 1)*(2(n + 1) + 1)}{6})
-
ore98
- Membre Naturel
- Messages: 11
- Enregistré le: 22 Mar 2015, 10:37
-
 par ore98 » 22 Mar 2015, 11:42
par ore98 » 22 Mar 2015, 11:42
Shew a écrit:On a
(2n + 1)}{6})
on traite donc n en fonction de l'indice de W :
*((n + 1) + 1)*(2(n + 1) + 1)}{6})
Oui mais la tunfait en fonction de n moi il me faut en fonction de Wn et ça je vois pas comment je peux faire
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 22 Mar 2015, 11:54
par Shew » 22 Mar 2015, 11:54
ore98 a écrit:Oui mais la tunfait en fonction de n moi il me faut en fonction de Wn et ça je vois pas comment je peux faire
:doh: :doh: ...
On connait
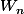
on connait (désormais)

en fonction de n, on peut facilement calculer

-
ore98
- Membre Naturel
- Messages: 11
- Enregistré le: 22 Mar 2015, 10:37
-
 par ore98 » 22 Mar 2015, 12:04
par ore98 » 22 Mar 2015, 12:04
Shew a écrit::doh: :doh: ...
On connait
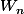
on connait (désormais)

en fonction de n, on peut facilement calculer

Je trouve pour resulta Wn+1-Wn=(5n^2+9n+4)÷6
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 22 Mar 2015, 12:08
par Shew » 22 Mar 2015, 12:08
ore98 a écrit:Je trouve pour resulta Wn+1-Wn=(5n^2+9n+4)÷6
Moi pas :lol3: . Vérifiez bien vos calculs, normalement la division disparait de l'expression .
-
ore98
- Membre Naturel
- Messages: 11
- Enregistré le: 22 Mar 2015, 10:37
-
 par ore98 » 22 Mar 2015, 12:11
par ore98 » 22 Mar 2015, 12:11
Shew a écrit:Moi pas :lol3: . Vérifiez bien vos calculs, normalement la division disparait de l'expression .
Apres vérification je trouve 5n^2+3n+2

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 22 Mar 2015, 12:11
par chan79 » 22 Mar 2015, 12:11
ore98 a écrit:Je trouve pour resulta Wn+1-Wn=(5n^2+9n+4)÷6
A mon avis, il s'agit de montrer que
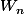
vérifie la relation de récurrence de la première question.
On montre que
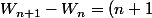^2)
ce qui amène au résultat
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 22 Mar 2015, 12:12
par Shew » 22 Mar 2015, 12:12
ore98 a écrit:Apres vérification je trouve 5n^2+3n+2
Posez tous vos calculs ici .
-
ore98
- Membre Naturel
- Messages: 11
- Enregistré le: 22 Mar 2015, 10:37
-
 par ore98 » 22 Mar 2015, 12:23
par ore98 » 22 Mar 2015, 12:23
Shew a écrit:Posez tous vos calculs ici .
Je vais commencé par la
((n+1)(n+2)(2n+2)-(n(n+1)(2n+1))÷6=((n+1)(2n^2+6n+4)-(n(2n^2+3n+1))÷6=((2n^3+8n^2+10n+4)-(2n^3+3n^2+n))÷6
=(8n^2+10n+4-3n^2-n)÷6=(5n^2+8n+4)÷6=5n^2+3n+2
-
mathelot
 par mathelot » 22 Mar 2015, 12:27
par mathelot » 22 Mar 2015, 12:27
factoriser
)
dans
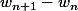 un peu d'Histoire:
un peu d'Histoire: pour calculer cette somme, un des Bernoulli (me rappelle plus lequel, ils étaient trois) a trouvé un polynôme de degré 3 ,
,)
bien déterminé, tel que
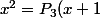-P_3(x))
ce qui a rendu cette somme de carrés télescopique.
Les termes de la somme sont des
nombres pyramidaux,car "sommer" revient à empiler des boulets de canon en carré de coté k (k=1,2...n)

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 22 Mar 2015, 12:28
par capitaine nuggets » 22 Mar 2015, 12:28
ore98 a écrit:Soit Un la suite definie pour tout entier naturel non nul de n par : Un=1^2+2^2+...+n^2
1) Donner l'expression de Un+1 en fonction de Un et le premier terme U1 de la suite
2) a) on considère maintenant la suite Wn definie par : Wn=(n×(n+1)(2n+1))÷6
Determiner W1 et Wn+1-Wn, puis l'expression de Wn+1 en fonction de Wn
b) en déduire que 1^2+2^2+...+n^2= (n×(n+1)(2n+1))÷6
Salut !
1)
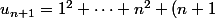^2)
et

donc

.
2)a) Sachant que la question suivante nous permet de montrer qu'en fait

, répondre à cette question revient à montrer que
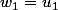
,
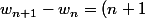^2)
(tu en déduis
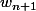
en fonction de
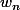
).
b) Pour en déduire que

, il suffit de montrer que :
[CENTER]
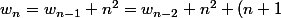^2=...=w_2+3^2+...+n^2=w_1+2^2+3^2+...+n^2=u_n)
[/CENTER]
-
ore98
- Membre Naturel
- Messages: 11
- Enregistré le: 22 Mar 2015, 10:37
-
 par ore98 » 22 Mar 2015, 12:32
par ore98 » 22 Mar 2015, 12:32
capitaine nuggets a écrit:Salut !
1)
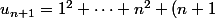^2)
et

donc

.
2)a) Sachant que la question suivante nous permet de montrer qu'en fait

, répondre à cette question revient à montrer que
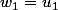
,
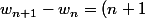^2)
(tu en déduis
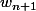
en fonction de
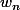
).
b) Pour en déduire que

, il suffit de montrer que :
[CENTER]
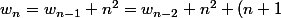^2=...=w_2+3^2+...+n^2=w_1+2^2+3^2+...+n^2=u_n)
[/CENTER]
Je comprend pas comment tu fait pour la question 2a
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 22 Mar 2015, 12:34
par Shew » 22 Mar 2015, 12:34
ore98 a écrit:Je vais commencé par la
((n+1)(n+2)(2n+2)-(n(n+1)(2n+1))÷6=((n+1)(2n^2+6n+4)-(n(2n^2+3n+1))÷6=((2n^3+8n^2+10n+4)-(2n^3+3n^2+n))÷6
=(8n^2+10n+4-3n^2-n)÷6=(5n^2+8n+4)÷6=5n^2+3n+2
Attention aux erreurs :
*((n + 1) + 1)*(2(n + 1) + 1)}{6} = \frac{(n + 1)*(n + 2)*(2n + 3)}{6})
-
ore98
- Membre Naturel
- Messages: 11
- Enregistré le: 22 Mar 2015, 10:37
-
 par ore98 » 22 Mar 2015, 12:41
par ore98 » 22 Mar 2015, 12:41
Shew a écrit:Attention aux erreurs :
*((n + 1) + 1)*(2(n + 1) + 1)}{6} = \frac{(n + 1)*(n + 2)*(2n + 3)}{6})
Je trouve donc n^2+2n+1=(n+1)^2
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 74 invités
) dans
dans 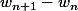
,) bien déterminé, tel que
bien déterminé, tel que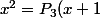-P_3(x))

et
donc
.
, répondre à cette question revient à montrer que
,
(tu en déduis
en fonction de
).
, il suffit de montrer que :
[/CENTER]
