Bonjour à tous.
J'aurais besoin d'un léger rappel. Mon but est de mettre sous forme algébrique ;)(1-3i), or j'ai oublié comment on s'y prend avec une racine carrée ^^'
Merci d'avance!
Nombres Complexes.
5 messages
- Page 1 sur 1
Salut !
Soit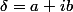 une racine carrée de
une racine carrée de  , i.e. un complexe tel que
, i.e. un complexe tel que 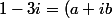^2) .
.
En identifiant partie réelle et partie imaginaire, montre que et
et  . Tu obtiens ainsi un système non linéaire de deux équations à deux inconnues où quatre solutions sont possibles :
. Tu obtiens ainsi un système non linéaire de deux équations à deux inconnues où quatre solutions sont possibles :
[CENTER] \\ 2ab= -3 & (E_2) \end{matrix} \end{cases}) [/CENTER]
[/CENTER]
Or seules deux le sont en fait, on a donc besoin d'une autre équation pour éliminer celles en trop.
En calculant le module de , déduis-en le module de
, déduis-en le module de  , puis finalement que
, puis finalement que  . On obtient ainsi un système non linéaire de trois équations à deux inconnues :
. On obtient ainsi un système non linéaire de trois équations à deux inconnues :
[CENTER] \\ 2ab= -3 & (E_2) \\ a^2+b^2=\sqrt{10} & (E_3) \end{matrix} \end{cases}) [/CENTER]
[/CENTER]
En te préoccupant seulement des équations) et
et ) , trouves les deux valeurs possibles pour
, trouves les deux valeurs possibles pour  et les deux valeurs possibles pour
et les deux valeurs possibles pour  .
.
(On a donc quatre solutions potentielles).
Or l'équation) te fournit l'information qui va te permettre de garder les bonnes solutions : elle te dit que les parties réelles et imaginaires des solutions doivent être de signe contraire.
te fournit l'information qui va te permettre de garder les bonnes solutions : elle te dit que les parties réelles et imaginaires des solutions doivent être de signe contraire.
P.S. : Evite d'écrire , en TS cela n'a à priori aucun sens puisque la fonction racine carrée est une fonction de
, en TS cela n'a à priori aucun sens puisque la fonction racine carrée est une fonction de  dans
dans  et non pas de
et non pas de  dans
dans  .
.
:+++:
Soit
En identifiant partie réelle et partie imaginaire, montre que
[CENTER]
Or seules deux le sont en fait, on a donc besoin d'une autre équation pour éliminer celles en trop.
En calculant le module de
[CENTER]
En te préoccupant seulement des équations
(On a donc quatre solutions potentielles).
Or l'équation
P.S. : Evite d'écrire
:+++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 42 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
