Exercices forme canonique
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
 par SecondeMathss » 15 Fév 2015, 16:38
par SecondeMathss » 15 Fév 2015, 16:38
Bonjour!
J'ai un problème: je dois faire un dm de maths pour mercredi, seulement je suis coincée aux deux premiers exercices...
J'ai essayé de déterminer la forme canonique des trinômes mais le problème c'est que j'ignore si j'ai bon (chose dont je doute) et je ne comprends pas comment calculer Béta
Pour l'exercice 1, A(x), j'ai trouvé A(x)= 1(x-(-3))²+14 avec Alpha = -3 et Béta = 14
Vous pensez que j'ai bon?

(
http://hpics.li/a9cb4e4 )
-
Manny06
- Membre Complexe
- Messages: 2125
- Enregistré le: 26 Jan 2012, 15:24
-
 par Manny06 » 15 Fév 2015, 17:00
par Manny06 » 15 Fév 2015, 17:00
SecondeMathss a écrit:Bonjour!
J'ai un problème: je dois faire un dm de maths pour mercredi, seulement je suis coincée aux deux premiers exercices...
J'ai essayé de déterminer la forme canonique des trinômes mais le problème c'est que j'ignore si j'ai bon (chose dont je doute) et je ne comprends pas comment calculer Béta
Pour l'exercice 1, A(x), j'ai trouvé A(x)= 1(x-(-3))²+14 avec Alpha = -3 et Béta = 14
Vous pensez que j'ai bon?

(
http://hpics.li/a9cb4e4 )
A(x)=x²-6x+5 =(x-3)²-4 refais tes calculs
-
Rizmoth
- Membre Naturel
- Messages: 74
- Enregistré le: 05 Fév 2015, 22:18
-
 par Rizmoth » 15 Fév 2015, 17:26
par Rizmoth » 15 Fév 2015, 17:26
Bonjour.
Pour l'exercice 1, A(x), j'ai trouvé A(x)= 1(x-(-3))²+14 avec Alpha = -3 et Béta = 14
Vous pensez que j'ai bon?
Comme Manny06 l'a remarqué, tu t'es trompé mais...
Vous pensez que j'ai bon?
Tu aurais pu facilement t'en rendre compte par toi-même en développant l'expression que tu avais trouvé !
En effet :
 = 1(x-(-3))^2+14)
 = (x + 3)^2+14)
 = x^2 + 6x + 9 +14)
 = x^2 + 6x + 23)
Tu vois bien que ce n'est pas ce que tu cherches, à savoir :

. Donc à refaire

On peut systématiser le calcul : pour passer de
^2 + \beta)
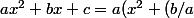x) + c)
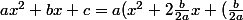^2) + c- (\frac{b}{2a})^2)
^2 + (c - \frac{b^2}{4a^2}))
En fin de compte, on a toujours :

et

Cordialement.
-
Robic
- Membre Irrationnel
- Messages: 1084
- Enregistré le: 03 Mai 2013, 11:00
-
 par Robic » 15 Fév 2015, 18:17
par Robic » 15 Fév 2015, 18:17
Attention, il est bien stipulé dans le programme que : « Savoir mettre sous forme canonique un polynôme de degré 2 nest pas un attendu du programme. » (Bulletin officiel n° 30 du 23 juillet 2009.)
Il me semble que, normalement, on utilise des formules toutes faites.
Ou alors le prof de maths fait du hors-programme ?
-
Rizmoth
- Membre Naturel
- Messages: 74
- Enregistré le: 05 Fév 2015, 22:18
-
 par Rizmoth » 15 Fév 2015, 18:34
par Rizmoth » 15 Fév 2015, 18:34
Ou alors le prof de maths fait du hors-programme ?
Vu la formulation de l'exercice, ça m'en a tout l'air...
Je ne comprends pas ce "nouveau" programme de seconde (je dis nouveau parce que ma seconde remonte à 2008-2009). A quoi ça sert de voir ces formes canoniques, alors qu'on verra en première les polynômes du second degré avec des outils bien plus puissants ?
C'est comme apprendre à skier sur des dunes de sables. ça peut marcher, mais c'est loin d'être indispensable...
Après je dis ça, je ne suis pas rédacteur de programme.
-
Robic
- Membre Irrationnel
- Messages: 1084
- Enregistré le: 03 Mai 2013, 11:00
-
 par Robic » 15 Fév 2015, 18:54
par Robic » 15 Fév 2015, 18:54
Si j'ai bien compris le but est d'avoir une première approche : on trace des paraboles, on voit qu'elles possèdent un axe de symétrie, un sommet, qu'on calcule avec une formule, ce genre de chose...
Mais tu as raison, l'énoncé semble suggérer qu'il doive se faire avec la méthode qui sera vue en première.
(Ou alors SecondeMathss n'est pas en seconde ?...)

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 15 Fév 2015, 19:19
par zygomatique » 15 Fév 2015, 19:19
salut
depuis la primaire on sait aussi que

donc

qu'on sait factoriser depuis le collège ...
:zen:
des programmes débiles oui .... mais l'objectif n'est plus d'instruire depuis bien longtemps ...

Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Robic
- Membre Irrationnel
- Messages: 1084
- Enregistré le: 03 Mai 2013, 11:00
-
 par Robic » 15 Fév 2015, 19:31
par Robic » 15 Fév 2015, 19:31
(Hors-sujet)
Je ne les trouve pas si débiles, les programmes, mais je trouve qu'ils favorisent trop souvent l'utilisation de formules toutes faîtes au détriment de la réflexion. Quelques exemples :
- La forme canonique se calcule maintenant avec des formules, même si le calcul en faisant apparaître une identité remarquable est quand même présenté en 1ère (à mon époque on ne voyait que ce calcul, pas de formules avec alpha et bêta).
- Pour déterminer l'équation de la tangente en une courbe (à partir de la dérivée), on enseigne la formule y = f'(a)(x-a) + f(a). À mon époque, on reconstituait l'équation en réfléchissant.
- En stats en seconde, on donne des formules toutes faites pour les intervalles de fluctuation, qu'on ne peut évidemment pas démontrer en seconde (ni même au lycée !). Est-ce que c'est vraiment des maths ?
- Je ne sais plus si la formule de la distance d'un point à un plan est toujours au programme de terminale, mais quelle idée d'obliger des élèves à apprendre une formule aussi indigeste (qu'ils ne sont pas obligés de comprendre, donc qu'ils ne comprennent pas) au lieu de les laisser dompter la 3D en faisant eux-mêmes les calculs.
Mais bon, il y a pire : les nouveaux programmes de physique, donc je ne me plains pas trop...

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 16 Fév 2015, 19:23
par zygomatique » 16 Fév 2015, 19:23
je te rejoins tout à fait ...
oui la réflexion peut se développer sur très peu de savoirs et "l'art" du calcul manuel peut y contribuer énormément ....
effectivement manipuler des formules incomprises n'a pas beaucoup de sens pour une instruction ... mise à part une illusion du savoir ...
on en voit ensuite les conséquences à bac + 1 avec un taux d'échec catastrophiques ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
yvelines78
- Membre Légendaire
- Messages: 6903
- Enregistré le: 15 Fév 2006, 21:14
-
 par yvelines78 » 17 Fév 2015, 14:59
par yvelines78 » 17 Fév 2015, 14:59
bonjour,
x²-3x-4
(x-3/2)²=x²-3x+9/4
--> x²-3x=(x-3/2)²-9/4
x²-3x-4=(x-3/2)²-9/4-4=(x-3/2)²-25/4 = forme cannonique
on peut continuer à factoriser
=(x-3/2)²-(5/2)²
a²-b²=(a-b)(a+b)
--> =[x-3/2-5/2][x-3/2+5/2]
=(x-8/2)(x+2/2)
=(x-4)(x+1)
-
Robic
- Membre Irrationnel
- Messages: 1084
- Enregistré le: 03 Mai 2013, 11:00
-
 par Robic » 17 Fév 2015, 15:34
par Robic » 17 Fév 2015, 15:34
Oui mais, encore une fois, le début est hors programme.
En fait, je m'aperçois que ce qui est difficile dans les exercices de lycée, ce n'est pas de les résoudre, mais de les résoudre en n'utilisant que les notions du programme ! :lol3: (c'est une boutade, hein... quoique...)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 53 invités
