Question sur le rayon
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
LINA82
- Membre Naturel
- Messages: 18
- Enregistré le: 19 Jan 2015, 02:56
-
 par LINA82 » 19 Jan 2015, 17:55
par LINA82 » 19 Jan 2015, 17:55
Bonjour
J'ai cet exercice
. Deux sphères sont découpées dans une roche uniforme. La première sphère a un rayon de 4.50cm. La masse de la deuxième est cinq fois plus grande que celle de la première. Déterminez le rayon de la deuxième sphère.
J'ai trouvera deux formules
volume=4/3pr3
Aire=4pr2
J'ai essayer de trouvera la masse de premier sphère et après je peux trouvera la masse de deuxième et peut être je peux trouver le rayon. Mais je suis perdu, comme je trouve pas une relation entre le rayon et la masse...
c'est quoi les formule que je peux utiliser pour résoudre mon problème
Merci a l'avance
-
mathelot
 par mathelot » 19 Jan 2015, 17:57
par mathelot » 19 Jan 2015, 17:57
on confond la masse et le volume d'une sphère (sauf si on connaissait la massse volumique de la roche, ce quui n'est pas le cas).
comme les volumes sont proportionnels à
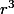
tu quotientes les deux cubes des rayons des sphères pour obtenir 5
En fait, tu utilise la proportionnalité avec la quantité
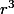
ça te permet de faire un calcul rapide!!!!
-
mathelot
 par mathelot » 19 Jan 2015, 18:19
par mathelot » 19 Jan 2015, 18:19

essaye un tableau de proportionnalité avec le cube des rayons....
malheureusement, il te faut la racine cubique (qui marche comme la racine carrée)
pour le chiffre 5
=2)
car
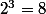
-
LINA82
- Membre Naturel
- Messages: 18
- Enregistré le: 19 Jan 2015, 02:56
-
 par LINA82 » 19 Jan 2015, 18:24
par LINA82 » 19 Jan 2015, 18:24
Merci, mais désoler j'ai pas bien compris la proportionnalité avec la quantité, ça veux dire quoi, pouvez vous m'expliquer pour la démarche me donner des indices pour que que je puisse commencer, merci
-
LINA82
- Membre Naturel
- Messages: 18
- Enregistré le: 19 Jan 2015, 02:56
-
 par LINA82 » 19 Jan 2015, 18:35
par LINA82 » 19 Jan 2015, 18:35
Merci, je veux essayer d'appliquer ce que vous m'avez dis. C'est apprécie
-
mathelot
 par mathelot » 19 Jan 2015, 18:49
par mathelot » 19 Jan 2015, 18:49
On fait le quotient des volumes
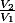
i) soit tu simplifies par 4/3 \pi, haut et bas dans le quotient
iii) mais la proportionnnalité "contient" cettte simplification

il suffit de multiplier l'ancien rayon 4.5cm par la racine cubique de 5.

-
WillyCagnes
- Membre Transcendant
- Messages: 3754
- Enregistré le: 21 Sep 2013, 19:58
-
 par WillyCagnes » 19 Jan 2015, 18:55
par WillyCagnes » 19 Jan 2015, 18:55
bsr
tu poses les 2 formules des volumes V1 et V2
V1= 4.Pi R1^3/3 1ère sphère de rayon R1
V2= 5.V1 = 5.[4.Pi.R1^3/3 ]= 4Pi.R2^3/3 2è sphère de rayon R2
on simplifie les 2 membres pour obtenir
5.R1^3 = R2^3
tu prends la racine cubique
(5^1/3).R1 = R2 rayon de la 2è sphère
1,71R1=R2
-
mathelot
 par mathelot » 19 Jan 2015, 19:00
par mathelot » 19 Jan 2015, 19:00
Il faut faire, commme les volumes sont dans un rappport de 5,
faire commme si 5 était un cube.
Si on avait 8 ou 27, pas de souci.
Là, on prends

comme coeffficient de proportionnnalité des rayons
c'est le seul nombre positif dont le cube vaut 5.
-
mathelot
 par mathelot » 19 Jan 2015, 19:08
par mathelot » 19 Jan 2015, 19:08
Avec les cubes solides, si tu veux que le cube_2 ait cinq fois
le volume du cube_.1, ça t'obliges à inventer de nouveaux nombres (

)
pour écrire le coefficient de proportionnalité entre les diagonales
-
LINA82
- Membre Naturel
- Messages: 18
- Enregistré le: 19 Jan 2015, 02:56
-
 par LINA82 » 19 Jan 2015, 19:46
par LINA82 » 19 Jan 2015, 19:46
Merci beaucoup je commence a comprendre, vous m'avez aider énormément , une chance que vous étés la,
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 61 invités
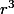
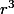 ça te permet de faire un calcul rapide!!!!
ça te permet de faire un calcul rapide!!!!