Petit exo de colle
15 messages
- Page 1 sur 1
petit exo de colle
Bonjour Soit P(X)=X^3+X-1 ave cP ;) C[ X] . On note x(k) ses trois racines complexes.
1) Vérifier (sans chercher à les calculer) que les 3 racines sont distinctes.
2) Effectuer la division euclidienne de X^5 par P .
j'aimerais surtout savoir la réponse ou un indice sur la première question que je ne cerne pas .. faut -il que je prouve que le discriminant est inférieur à 0? merci...
1) Vérifier (sans chercher à les calculer) que les 3 racines sont distinctes.
2) Effectuer la division euclidienne de X^5 par P .
j'aimerais surtout savoir la réponse ou un indice sur la première question que je ne cerne pas .. faut -il que je prouve que le discriminant est inférieur à 0? merci...
Salut !
Tu t'es trompé, il faut faire la division euclidienne de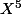 par
par  et non pas l'inverse ; puis
et non pas l'inverse ; puis +X^{2}+X-1 = X^7-X^5+X^{2}+X-1 \ne X^3+x-1)
:+++:
maestro_ a écrit:et c'est quoi le rapport avec la question 2 si on ne calcule pas ses racines moi je trouve
Tu t'es trompé, il faut faire la division euclidienne de
:+++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
salut
une autre approche
On voit facilement qu'il y a une racine réelle a et deux racines non réelles
Supposons que les deux racines non réelles soient égales (à b)
(x-b)²(x-a)=x³+x-1
(x²-2bx+b²)(x-a)=x³+x-1
En identifiant les coefficients de x², on a -a-2b=0 impossible car b serait un réel
correction effectuée
une autre approche
On voit facilement qu'il y a une racine réelle a et deux racines non réelles
Supposons que les deux racines non réelles soient égales (à b)
(x-b)²(x-a)=x³+x-1
(x²-2bx+b²)(x-a)=x³+x-1
En identifiant les coefficients de x², on a -a-2b=0 impossible car b serait un réel
correction effectuée
chan79 a écrit:salut
une autre approche
On voit facilement qu'il y a une racine réelle a et deux racines non réelles
Supposons que les deux racines égales non réelles soient égales (à b)
(x-b)²(x-a)=x³+x-1
(x²-2bx+b²)(x-a)=x³+x-1
En identifiant les coefficients de x², on a -a-2b=1 impossible car b serait un réel
salut
j'allais proposer cela quand j'ai vu ton post...
on n'est même pas obligé de savoir qu'une racine est réelle ....
si les trois racines ne sont pas distinctes alors au moins deux sont confondues donc P(x) = (x - a)(x - b)² = x^3 + x - 1
ensuite c'est plutôt :: -a - 2b = 0 (car il n'y a pas de x² ....)
autre argument : le polynome est à coeficient réels et le produit de racines est - 1 donc a et b sont conjuguées ....
sinon on peut poser la division euclidienne ....
:lol3:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
15 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 65 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
