Soient le vecteur de R3 , u1=(1,1,1) , u2=(2,1,1)
1-montrez que la famille {u1,u2} est libre : resolu
2- soit a un reel on considere l'ensemble
F2={(x,y,z) appartient R3 , x-3y+z=a}
pour quelle valeur de a , Fa est un sous espace vectoriel de R3
3- montrez que F0 est un sous espace vectoriel de R3 de dimension inferieur ou egale a 2
donner une base a F0 quelle est sa dimension
Avec explication svp et merci d'avance.. ^^
Espace vectoriel
5 messages
- Page 1 sur 1
Salut !
2- (0,0,0) doit être un élément de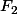 :+++:
:+++:
3- C'est quoi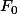 ?
?
reyo94 a écrit:Soient le vecteur de R3 , u1=(1,1,1) , u2=(2,1,1)
1-montrez que la famille {u1,u2} est libre : resolu
2- soit a un reel on considere l'ensemble
F2={(x,y,z) appartient R3 , x-3y+z=a}
pour quelle valeur de a , Fa est un sous espace vectoriel de R3
3- montrez que F0 est un sous espace vectoriel de R3 de dimension inferieur ou egale a 2
donner une base a F0 quelle est sa dimension
Avec explication svp et merci d'avance.. ^^
2- (0,0,0) doit être un élément de
3- C'est quoi
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
reyo94 a écrit:aa Fa alors.. merci pour premier question :lol3:
Bonjour, du coup on a :
On peut considérer l'application linéaire
On a donc
Si on écrit
Et les deux vecteurs utilisés sont bien libres...
Après on peut certainement utiliser ceux du départ, faut regarder ce que ça donne...
BiancoAngelo a écrit:Bonjour, du coup on a :
On peut considérer l'application linéairedéfinie par :
, on a alors
On a doncd'où
par théorème du rang...
Si on écrit
Et les deux vecteurs utilisés sont bien libres...
Après on peut certainement utiliser ceux du départ, faut regarder ce que ça donne...
Merci c'est trés bien expliquer..
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
