Vous reprendrez bien d'un peu d'exponentielle ?

[praste]

Salutations,

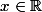
Au détour d'une malencontreuse démonstration, il me faut montrer qu'il existe un vérifiant, pour tout tel que :

[CENTER][/CENTER]

Voilà qui semble en apparence abordable ; pourtant, je dois avouer que je ne sais pas trop par où partir. Si vous avez des pistes de réflexion à me faire parvenir, ce serait avec grand plaisir.

Joyeuse fin de journée.

[Ben314]

Salut,
Si tu veut pas te faire c..., tu étudie bêtement les fonctions et au voisinage de 0.

[Luc]

Salutations,

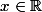
Au détour d'une malencontreuse démonstration, il me faut montrer qu'il existe un vérifiant, pour tout tel que :

[CENTER][/CENTER]

Voilà qui semble en apparence abordable ; pourtant, je dois avouer que je ne sais pas trop par où partir. Si vous avez des pistes de réflexion à me faire parvenir, ce serait avec grand plaisir.

Joyeuse fin de journée.

Bonjour praste,

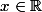
L'inégalité de gauche est vraie pour tout . (étude de fonction)
Celle de droite est vraie uniquement localement en 0 (étude de fonction)

[BiancoAngelo]

Salutations,

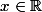
Au détour d'une malencontreuse démonstration, il me faut montrer qu'il existe un vérifiant, pour tout tel que :

[CENTER][/CENTER]

Voilà qui semble en apparence abordable ; pourtant, je dois avouer que je ne sais pas trop par où partir. Si vous avez des pistes de réflexion à me faire parvenir, ce serait avec grand plaisir.

Joyeuse fin de journée.

Bonsoir,

Si on veut montrer qu'il existe un vérifiant , on peut ramener cette inégalité à vérifier à la résolution de l'inéquation




Si x est proche de 0, on peut prendre le ln...:




Allez, je pose (définie "vers" 0)

qui change de signe en 0... f atteint un maximum en 0... qui vaut... 0. OK pour le côte gauche.

Allez, je pose (vers 0 aussi).

qui change de signe en 0... g atteint un minimum en 0... qui vaut 0. OK pour le côté droit.

Evidemment, tout ça vers 0.

Donc c'est OK :lol3: