Ensemble bien ordonné

par **Clise** » 08 Juil 2008, 19:15

ok, donc j'en conclus que ça marche pas si c'est infini et que ça marche si c'est finit ...

Pour prouver que c'est bien ordonné dans le cas finit on prend les termes de F ayant plus petit élément du plus grand indice et après ?

par **aviateurpilot** » 08 Juil 2008, 19:26

j'ai montrer l'existence et l'unicité
t'a pas vu que pour tout k

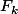
est non vide !!

par **leon1789** » 08 Juil 2008, 19:29

aviateurpilot a écrit:j'ai montrer l'existence et l'unicité
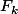
t'a pas vu que pour tout k est non vide !!

C'est l'intersection des F_k qui contien(drai)t l'élément cherché.

par **Clise** » 08 Juil 2008, 19:29

Dans, ce cas si ta démonstration est juste, alors pourquoi il existe un contre exemple ?

par **aviateurpilot** » 08 Juil 2008, 19:32

Clise a écrit:Dans, ce cas si ta démonstration est juste, alors pourquoi il existe un contre exemple ?

dans ma demo, a montrer l'existence et l'unicité du plus petit element dans F,
d'apres la definion que j'ai vu sur wikipedia E est bien ordonné

par **Clise** » 08 Juil 2008, 19:45

J'ai consulté ces pages et vu seulement que (N,<) était bien ordonné pas N^N, mais je peux me tromper ...

par **leon1789** » 08 Juil 2008, 19:46

aviateurpilot a écrit:dans ma demo, a montrer l'existence et l'unicité du plus petit element dans F,
d'apres la definion que j'ai vu sur wikipedia E est bien ordonné

Où as-tu prouvé que l'élément minimal appartient à F ? ou si tu préfères que l'intersection des F_k est non vide ?

par **leon1789** » 08 Juil 2008, 19:48

Clise a écrit:J'ai consulté ces pages et vu seulement que (N,<) était bien ordonné pas N^N, mais je peux me tromper ...

Tu ne te trompes pas : N^N est équipotent à R , qui est réputé ne pas avoir de bon ordre... quel que soit l'ordre total considéré...

par **nuage** » 08 Juil 2008, 19:54

Salut,
Si on accepte l'axiome du choix, tout ensemble peut-être muni d'un bon ordre.

par **leon1789** » 08 Juil 2008, 19:57

heu... oui, c'est vrai ... :marteau: pourtant je croyais.. bon,ben, ça fait du bien de revoir les fondamentaux :triste:

par **Clise** » 08 Juil 2008, 19:58

donc si on accepte l'axiome du choix, ça fait que N^N est bien ordonné ? comprends plus grand chose la ... :mur:

Quand est il alors du contre exemple proposé plus haut ?

Mais je veux pas prouvé qu'il existe un bon ordre, mais que c'est bien ordonné avec l'ordre lexicographique ...

par **leon1789** » 08 Juil 2008, 19:59

Clise a écrit:donc si on accepte l'axiome du choix, ça fait que N^N est bien ordonné ? comprends plus grand chose la ... :mur:

...ça fait que N^N est bien ordonné, pour un ordre bien choisi ! Pas celui de ton exo (cf le contre-exemple)
D'ailleurs, un bon ordre pour N^N va être assez peu intuitif je pense. :id:

par **nuage** » 08 Juil 2008, 20:02

Hors sujet

par **leon1789** » 08 Juil 2008, 20:04

nuage a écrit:Hors sujet

Que veux-tu dire ?

par **Clise** » 08 Juil 2008, 20:04

ok, donc revenons au sujet initial ? :we:

si la séquence des entiers est infinie dans ce cas en expliquant le contre exemple décrit plus haut, on prouve que N^N n'est pas ordonné.

Dans le cas finit c'est a dire pour N^n, on a un bon ordre (je suppose), mais j'arrive pas a le prouver "formellement" ... :hum:

pourquoi hors sujet?

par **leon1789** » 08 Juil 2008, 20:07

Clise a écrit:Dans le cas finit c'est a dire pour N^n, on a un bon ordre (je suppose), mais j'arrive pas a le prouver "formellement" ... :hum:

Prends le F_k de AviateurPilot.

par **Clise** » 08 Juil 2008, 20:09

Donc le plus petit élément possible appartient à Fn qui est non vide ... ok
on a prouvé l'uncité et l'existence la je crois, non ?

par **leon1789** » 08 Juil 2008, 20:42

Clise a écrit:Donc le plus petit élément possible appartient à Fn qui est non vide ... ok
on a prouvé l'uncité et l'existence la je crois, non ?

oui je crois.

par **Clise** » 08 Juil 2008, 20:47

et alors, (je sais je chipote un peu mais je veux être sure de bien avoir tout compris...) pourquoi dans le cas infini ce que aviateurpilot ne marche pas pour l'existence ? si tous les Fk sont vides a l'infini il ne devrait pas en exister un au moins ?

par **leon1789** » 08 Juil 2008, 20:50

Clise a écrit:et alors, (je sais je chipote un peu mais je veux être sure de bien avoir tout compris...) pourquoi dans le cas infini ce que aviateurpilot ne marche pas pour l'existence ? si tous les Fk sont vides a l'infini il ne devrait pas en exister un au moins ?

On ne dit pas si tous les Fk sont vides a l'infini (enfin, je ne crois pas qu'on le dise...)
Je suppose que tu veux dire si tous les Fk sont non vides a l'infini...
Cela se dit si l'intersection de tous les Fk est non vide !
Et justement, il y a un "si" qui n'est pas toujours réalisé (cf contre exemple)

Ensemble bien ordonné

Qui est en ligne