Fonction exponentielle et dérivation

[Seb1510]

Bonsoir, j'ai deux exercice impossible pour moi, à vous présenter :

Ex 1 : f définie sur IR par : f(x) = (x² + x-1)ex
On note f^(1) = f', f^(2) = f''
1. Calculer pour tout réel x, f' et f''.
2. Démontrer par récurrence que pour tout entier n>= 1,
f^(n) = x²+anx+bn)ex avec an+1 = an+2
et bn+1 = an+bn
3. On se propose dans cette question d'exprimer an et bn en fonction de n.
a) Quelle est la nautre de la suite (an) ? En déduire an en fonction de n pour tout entier n>=1.
b)Vérifier que pour tout n>=1: bn= aan-1+an-2+...+a2+a1
En déduire bn en fonction de n pour tout entier n>=1
Merci de votre aide.

[capitaine nuggets]

Salut !

Bonsoir, j'ai deux exercice impossible pour moi, à vous présenter :

Ex 1 : f définie sur IR par : f(x) = (x² + x-1)ex
On note f^(1) = f', f^(2) = f''
1. Calculer pour tout réel x, f' et f''.
2. Démontrer par récurrence que pour tout entier n>= 1,
f^(n) = x²+anx+bn)ex avec an+1 = an+2
et bn+1 = an+bn
3. On se propose dans cette question d'exprimer an et bn en fonction de n.
a) Quelle est la nautre de la suite (an) ? En déduire an en fonction de n pour tout entier n>=1.
b)Vérifier que pour tout n>=1: bn= aan-1+an-2+...+a2+a1
En déduire bn en fonction de n pour tout entier n>=1
Merci de votre aide.

Où bloques-tu ?
Qu'as tu fait pour le moment ?
C'est bête que tu ne l'aies pas précisé : les deux premières questions sont assez claires et pas spécialement compliquées. Du coup, j'ai un peu de mal à voir quelles indications te donner...
Ensuite, la question 3.a) n'est qu'une application du cours (à noter que si on demande une nature de suite, c'est qu'elle doit être probablement arithmétique ou géométrique, étant donné le peu de suite différentes à connaître).
3.b) En remarquant, d'après la question 2., que quel que soit , qu'on veut la somme de jusqu'à , calcule 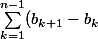(les termes du membre de droite de cette égalité vont se simplifier :+++: ).
Enfin, est la suite de termes consécutifs d'une suite dont la nature est à trouver à la question 2.a), dont le premier terme est ... et de raison ... donc tu dois avoir une formule dans le cours qui te donnera :lol3:

[Seb1510]

Tes indications donnés était pile celle qu'il me fallait !!! :p
J'ai juste un autre exo qui dure 1 question.. :
z=x+iy
Z = z-2z(barre) +2
Calculer Z et trouver la partie Re(Z) et la partie Im(Z). Fait : Z = -x+2 +3iy
Mais la question deux :
Résoudre dans C l'équation Z = 0 d'inconnue z, et là est mon problème, je tombe sur un calcule avec un produit en (3i) en dénominateur d'une fraction et ne plus avançait...
Mais si tu pouvais m'aider à résoudre cette équation.. ^^
C'est des imaginaires et non plus de la fonction exponentielle ^^

[capitaine nuggets]

Tes indications donnés était pile celle qu'il me fallait !!! :p
J'ai juste un autre exo qui dure 1 question.. :
z=x+iy
Z = z-2z(barre) +2
Calculer Z et trouver la partie Re(Z) et la partie Im(Z). Fait : Z = -x+2 +3iy
Mais la question deux :
Résoudre dans C l'équation Z = 0 d'inconnue z, et là est mon problème, je tombe sur un calcule avec un produit en (3i) en dénominateur d'une fraction et ne plus avançait...
Mais si tu pouvais m'aider à résoudre cette équation.. ^^
C'est des imaginaires et non plus de la fonction exponentielle ^^

Z = 0 si et seulement si Re(Z) = 0 ET Im(Z) = 0 :+++: