Exponentielle et dérivation
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 25 Juin 2009, 19:55
par Dinozzo13 » 25 Juin 2009, 19:55
bonsoir, j'aurais besoin de votre aide pour lever un doute. Si on a
=e^{-t})
, a-t-on
=-e^{-t})
et
=[f'(t)]'=e^{-t}=f(t))
?
-
variobike01
- Membre Relatif
- Messages: 148
- Enregistré le: 06 Sep 2007, 20:39
-
 par variobike01 » 25 Juin 2009, 20:07
par variobike01 » 25 Juin 2009, 20:07
Salut,
Moi effectivement je trouve bien ça ^^
Après à prendre avec des pincettes car je n'ai pas encore vu les exponentielles ... :zen:
++
Rémi
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 25 Juin 2009, 20:10
par Dinozzo13 » 25 Juin 2009, 20:10
ok je vous remercie :ptdr:
-
uztop
- Membre Complexe
- Messages: 2396
- Enregistré le: 12 Sep 2007, 11:00
-
 par uztop » 25 Juin 2009, 20:13
par uztop » 25 Juin 2009, 20:13
Salut,
je confirme ce que dit Rémi :)
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 25 Juin 2009, 20:14
par Dinozzo13 » 25 Juin 2009, 20:14
:ptdr: merci
-
variobike01
- Membre Relatif
- Messages: 148
- Enregistré le: 06 Sep 2007, 20:39
-
 par variobike01 » 25 Juin 2009, 20:23
par variobike01 » 25 Juin 2009, 20:23
Tiens d'ailleurs tant que nous somme sur ce sujet.
On peut alors dire de cette fonction que sa classe est infinie non ? (simple question voir si j'ai bien compris le principe)
++
Rémi
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 25 Juin 2009, 20:37
par Dinozzo13 » 25 Juin 2009, 20:37
Ah désolé, je n'ai pas encore aborder la notion de "classe" :doh:
-
variobike01
- Membre Relatif
- Messages: 148
- Enregistré le: 06 Sep 2007, 20:39
-
 par variobike01 » 25 Juin 2009, 20:40
par variobike01 » 25 Juin 2009, 20:40
Ben je crois que la classe d'une fonction quantifie le nombre de fois ou elle est dérivable ...
Donc ici, une infinité de fois ^^ Donc classe infinie ...
++
Rémi
-
uztop
- Membre Complexe
- Messages: 2396
- Enregistré le: 12 Sep 2007, 11:00
-
 par uztop » 25 Juin 2009, 20:42
par uztop » 25 Juin 2009, 20:42
variobike01 a écrit:Tiens d'ailleurs tant que nous somme sur ce sujet.
On peut alors dire de cette fonction que sa classe est infinie non ? (simple question voir si j'ai bien compris le principe)
++
Rémi
oui on peut. Pour Dinozzo13, une fonction de classe infinie (notée

) est une fonction qui est dérivable une infinité de fois.
En pratique, toutes les fonctions vues au lycée (polynômes, exponentielles, logs, fonctions trigo, ...) sont

-
uztop
- Membre Complexe
- Messages: 2396
- Enregistré le: 12 Sep 2007, 11:00
-
 par uztop » 25 Juin 2009, 20:45
par uztop » 25 Juin 2009, 20:45
variobike01 a écrit:Ben je crois que la classe d'une fonction quantifie le nombre de fois ou elle est dérivable ...
Donc ici, une infinité de fois ^^ Donc classe infinie ...
++
Rémi
en fait, il faut aussi que la dérivée soit continue. Par exemple, une fonction

est dérivable une fois et sa dérivée est continue.
Mais ça ne change absolument rien pour les fonctions

-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 25 Juin 2009, 20:45
par Dinozzo13 » 25 Juin 2009, 20:45
compréhensible et intuitivement évident cette notion de classe infinie, merci pour la culture :ptdr: .
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 25 Juin 2009, 20:47
par Dinozzo13 » 25 Juin 2009, 20:47
dites Uztop, y a-t-il des cas particuliers :ptdr:
-
uztop
- Membre Complexe
- Messages: 2396
- Enregistré le: 12 Sep 2007, 11:00
-
 par uztop » 25 Juin 2009, 20:53
par uztop » 25 Juin 2009, 20:53
des fonctions qui ne soient pas

?
Oui, il y en a plein, un exemple simple est f(x) = |x|
f est continue mais elle n'est pas dérivable en 0, il s'agit donc d'une fonction
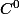
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 25 Juin 2009, 20:58
par Dinozzo13 » 25 Juin 2009, 20:58
petite précision, si le domaine de définition comporte des valeurs interdites, alors une fonction n'est pas de classe infinie parce qu'elle n'est pas dérivable en certains points mais aussi parce qu'elle n'est pas continue.
-
uztop
- Membre Complexe
- Messages: 2396
- Enregistré le: 12 Sep 2007, 11:00
-
 par uztop » 25 Juin 2009, 21:03
par uztop » 25 Juin 2009, 21:03
on parle de la classe d'une fonction sur son intervalle de définition. S'il y a des valeurs interdites, elles ne sont pas dans l'intervalle de définition et ne posent donc pas de problème de ce point de vue là.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 25 Juin 2009, 21:05
par Dinozzo13 » 25 Juin 2009, 21:05
d'accord merci pour la leçon :ptdr:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités
=e^{-t}) , a-t-on
, a-t-on =-e^{-t}) et
et =[f'(t)]'=e^{-t}=f(t)) ?
?