Bonjour à tous et à toutes,
Une question à mon examen est tombé et j'ai eu 0 point car je n'ai pas respecté la consigne comme il le fallait . La voici : En posant un changement de variable judicieux calculer l'intégrale suivante pour A appartenant à R+ : Intégrale de 1 à A de f(x) . Tout en sachant que f(x) = 1 / (x(1+ln(x)²)).
J'ai calculé sans changement de variable car je ne trouvais pas ça utile , j'ai trouvé pi.4, plus précisément F(e) .
Avec tout votre respect, je vous embête afin de savoir comment auriez-vous calculer cela avec un changement de variable ?
Coordialement
Navid
Changement de variable ridicule
9 messages
- Page 1 sur 1
La fonction à intégrer est de la forme  en posant
en posant  = \ln x) donc, effectivement, on peut calculer directement une primitive. J'imagine que le changement de variable attendu était
donc, effectivement, on peut calculer directement une primitive. J'imagine que le changement de variable attendu était  mais c'est un peu tordu d'appeler ça un changement de variable dans un cas aussi simple. (À la fin je trouve
mais c'est un peu tordu d'appeler ça un changement de variable dans un cas aussi simple. (À la fin je trouve ) . Peut-être que tu as eu 0 parce que tu n'as pas trouvé le bon résultat ?)
. Peut-être que tu as eu 0 parce que tu n'as pas trouvé le bon résultat ?)
Ou alors il y a quelque chose qui m'a échappé ?
Ou alors il y a quelque chose qui m'a échappé ?
Je peux vous citer les questions juste avant cette question, peut-être que cela vous aidera . '' Montrer que la fonction est dérivable . '' , '' En déduire le tableau de variation '' , ''Tracer sa courbe '', '' Montrer que la fonction F est définie par F(x)= artcan(ln(x)) est une primitive de la fonction f '' , '' Calculer F(1) et F(e^1)'', '' Rprésenter graphiquement l'intégrale suivante puis la calculer : Intégrale de e^1 à 1 de f(x) '' . Voici les questions dans l'ordre
Apparemment votre réponse est juste, je vous remercie . Par contre avais-je le droit de mettre directement de la sorte : F(A) - F(1) = F(A) - 0 = F(A) ?
Apparemment votre réponse est juste, je vous remercie . Par contre avais-je le droit de mettre directement de la sorte : F(A) - F(1) = F(A) - 0 = F(A) ?
salut
je ne vois pas l'intérêt de faire un changement de variable puisque les questions précédentes donne une primitive qui s'obtient par ce changement de variable et que pour prouver que c'est une primitive il suffit de dériver ...
on peut donc directement répondre F(A) - F(1) = F(a) ...
maintenant je ne vois pas la même question dans ton premier et dernier post ....
je ne vois pas l'intérêt de faire un changement de variable puisque les questions précédentes donne une primitive qui s'obtient par ce changement de variable et que pour prouver que c'est une primitive il suffit de dériver ...
on peut donc directement répondre F(A) - F(1) = F(a) ...
maintenant je ne vois pas la même question dans ton premier et dernier post ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Bonjour
Quand tu as posé = \ln x) , tu as implicitement fait le changement de variables
, tu as implicitement fait le changement de variables  on a alors
on a alors dx=du) et
et dx}{1+u^2(x)}= \int_{u(1)}^{u(A) }\dfrac{du}{1+u^2}) .
.
Concernant la question avec le changement de variables, on peut la traiter de tous les noms, il n'empêche qu'il fallait répondre à la question posée (même si le résultat de l'intégration est déjà connu, travail mâché avant).
Qu'en serait-il si l'exercice ne contenait que cette question?
Ps: Le 0 qu'a eu persiiian ne concernait que la dernière question (calculer)}) avec un changement de variables adéquat), et je pense qu'il est légitime puisqu'il a jugé inutile de faire le changement de variables.
avec un changement de variables adéquat), et je pense qu'il est légitime puisqu'il a jugé inutile de faire le changement de variables.
Robic a écrit:La fonction à intégrer est de la forme [TEXtex]\frac{u'}{1+u^2}[/tex] en posantdonc, effectivement, on peut calculer directement une primitive.
Quand tu as posé
Concernant la question avec le changement de variables, on peut la traiter de tous les noms, il n'empêche qu'il fallait répondre à la question posée (même si le résultat de l'intégration est déjà connu, travail mâché avant).
Qu'en serait-il si l'exercice ne contenait que cette question?
Ps: Le 0 qu'a eu persiiian ne concernait que la dernière question (calculer
deltab : je comprends bien que j'ai fait implicitement un changement de variable. Je disais juste que lorsque c'est aussi simple, on ne dit pas « faire un changement de variable ».
Par exemple voici une intégrale :
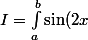 \, dx) .
.
Je serais un peu surpris si on me disait : « avec un changement de variable adéquat, calculer I » sous prétexte que dans la recherche de la primitive, on pose implicitement u(x) = 2x et du coup u'(x) dx = du, etc. Pour moi, j'ai juste utilisé une primitive connue, celle de u' sin u. Pareil dans cet exercice avec u'/[1+u²].
Par exemple voici une intégrale :
Je serais un peu surpris si on me disait : « avec un changement de variable adéquat, calculer I » sous prétexte que dans la recherche de la primitive, on pose implicitement u(x) = 2x et du coup u'(x) dx = du, etc. Pour moi, j'ai juste utilisé une primitive connue, celle de u' sin u. Pareil dans cet exercice avec u'/[1+u²].
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 38 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
