Endomorphisme

[med bah]

salut tout le monde:
s'il vous plait je bloque dans la deuxième question ,
Soient n N
, E = Rn [X] et l'endomorphisme de E déterminé par
(P) = P(X + 1) P(X).
a) Justi;)er que l'endomorphisme est nilpotent.
b) Déterminer des réels a0, . . . , an, an+1 non triviaux véri;)ant P Rn [X]:
n+1
;)akP(X + k) = 0
k=0
Merci pour votre aide

[carp-sarah]

D c'est delta

si P est de degré k inferieur ou egale a n, alors D(P) est de degré k-1, donc si tu appliques D k fois, t'obtiens Dk (P)=0 en général, on est sur que Dn(P) = 0

[barbu23]

Une autre alternative :
Exhiber une base de dans laquelle la matrice de est
De mémoire, c'est :
avec une famille de polynômes définies par récurrence :
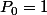
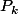
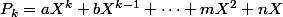
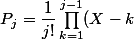et qui donnent et et ainsi de suite. Il faut choisir de la forme , parce que : , ensuite, on cherche , puis on factorise ( c'est pas évident la phase de factorisation, mais il suffit de le faire pour , et tu en déduis la formule par récurrence, c'est à dire : ). C'est facile.

[Ben314]

Perso, pour la deuxième question, je t'inciterais assez fortement à commencer par regarder qui sont ;)^2, ;)^3, ;)^4 puis de conjecturer qui est ;)^n et de démontrer ta conjecture par récurrence. (vu la question 1) où tu as montré que ;)^n=0, la formule qu'on te demande d'exhiber au 2), c'est évidement celle de ;)^n)
Ce n'est certe pas la méthode la plus esthétique, mais je pense que c'est assez instructif.

Pour te donner le début (je me foule pas trop...) :

;)(P)(X) = P(X+1) - P(X)

;)²(P)(X) = ;)(;)(P))(X) = ;)(P)(X+1) - ;)(P)(X) = [P(X+2)-P(X+1)] - [P(X+1)-P(X)] = P(X+2) - 2P(X+1) + P(X)

;)^3(P)(X) = ;)(;)²(P))(X) = ;)²(P)(X+1) - ;)²(P)(X)
etc...

Aprés, une fois que tu as montré le résultat par récurrence, tu peut essayer de voir s'il n'y avait pas une façon plus "jolie" de le trouver (il y en a... plusieurs..., par exemple celle de Barbu...)