Bonjour, il y a peut-être un souci de terminologie : a priori le portrait de phase de ton système c'est un ensemble de courbes qui vivent dans l'espace des phases à 4 dimensions (x,y,x',y'), donc c'est pas évident à dessiner (tu peux en dessiner des sections). En revanche, et c'est ce que tu as l'air de suggérer, tu peux dessiner les lignes de niveau de ton hamiltonien dans le plan (x,y). Comme dans ton cas le hamiltonien ne dépend que de x et de y ça revient au portrait de phase dans (x,x'). Dans le cas général c'est moins détaillé que le portait de phase mais ça permet déjà de visualiser un certain nombre d'informations sur le comportement de ton système ; notamment comme l'a dit aviateur de voir les points d'équilibre, leur nature et les principaux régimes possibles (états libres, états liés, restrictions sur l'espace qui peut être "exploré" par une trajectoire donnée, etc).
Tu peux réecrire les lignes de niveau sous la forme
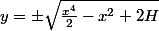
, ça se trace bien.
Edit : au temps pour moi je suis allé trop vite en lisant les notations. J'ai trop l'habitude de travailler avec des notations du type
)
qui font explicitement apparaître le lien entre les variables et leur dérivée. Du coup c'est bien du portrait de phase dont on parle, l'espace des phases est le plan (x,y) et le système physique sous-jacent a un seul degré de liberté (x).


