J'ai un nouveau problème,
Je dispose de
 = \left( \pi\sigma^2\hbar^2 \right)^{-\frac{1}{4}} \exp\left(-\frac{(p-p_0)^2}{2\sigma^2\hbar^2}\right))
un paquet d'onde gaussien.
La question en amont consiste à montrer qu'on a
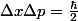
pour t=0. Mon premier soucis est de calculer les quantités
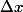
et
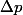
qui peuvent être interprétés comme étant les écart-types (dispersions) des grandeurs x et p, se définissant ainsi :
^2 = \langle x^2\rangle - \langle x\rangle^2)
Pour ce faire, j'ai besoin de calculer
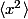
et
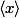
, accessibles seulement par le calcul de la fonction d'onde

car en 1-D, le centre de la distribution formant le paquet d'onde correspond à
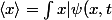|^2 \mathrm{d}x)
.
Or
 = \frac{1}{\(2\pi \hbar\)^{\frac{3}{2}}} \int \phi(\bar p) e^{i\(\bar p\cdot \bar r - Et\)/\hbar} \mathrm{d}^3 p)
, et pour t = 0, selon la composante x, on a ici :
 = \frac{1}{\(2\pi \hbar\)^{\frac{3}{2}}} \int \phi(p) e^{ipx/\hbar} \mathrm{d} p)
En remplaçant
)
dans cette équation, j'ai :
 = \frac{\( \pi \sigma^2 \hbar^2\)^{-\frac{1}{4}}}{\(2\pi \hbar\)^{\frac{3}{2}}} \int e^{-\frac{(p-p_0)^2}{2\sigma^2\hbar^2}} e^{ipx/\hbar} \mathrm{d} p)
et le corrigé succinct indique qu'il faut aboutir à
 = \(\frac{\sigma^2}{\pi}\)^{\frac{1}{4}}e^{ip_0x/\hbar}e^{-x^2\sigma^2/2})
.
Pour l'instant, j'ai essayé un timide changement de variable
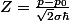
sans doute dans l'espoir inconscient de me retrouver avec l'intégrale d'une gaussienne. Cette maigre tentative a l'air encourageante puisque je me retrouve avec
^{-\frac{1}{4}}}{\(2\pi \hbar\)^{\frac{3}{2}}}\int e^{-Z^2} e^{i\sqrt{2}\sigma Z}e^{ip_0x/\hbar}\times \sqrt{2}\sigma \hbar \mathrm{d}Z)
mais là, le terme
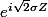
m'interroge beaucoup. Comment m'en sortir ?