Une série d'exercices d'entraînement (niveau lycée bien ente
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 25 Oct 2009, 20:24
par Timothé Lefebvre » 25 Oct 2009, 20:24
Ah ah benekire je t'ai vu parler de matrices !
Deux exos en relation avec celles-ci mais toujours sans les nommer (on est quand même encore au lycée !)
Énoncé 7 (système) :Résoudre le système d'inconnue a et b tq
 \in \mathbb{C}^2)
:
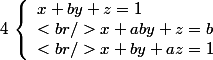 Énoncé 8 (système et paramètre) :
Énoncé 8 (système et paramètre) :Pareil, dans

et de paramètre m :
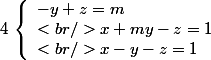
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 25 Oct 2009, 20:39
par Zweig » 25 Oct 2009, 20:39
Tant qu'on est sur les systèmes :
Résoudre dans
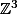
:

-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 25 Oct 2009, 20:43
par Timothé Lefebvre » 25 Oct 2009, 20:43
Argh, le renard de feu est récalcitrant ce soir, il ne veut pas me montrer ton système !
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 25 Oct 2009, 21:46
par Timothé Lefebvre » 25 Oct 2009, 21:46
Timothé Lefebvre a écrit:Énoncé 4 (système) :Soit (S) le système suivant, tq

et de paramètre a tq

:

Indice : étude de cas sur les valeurs possibles de a (choisir quatre cas différents).
Correction :
Le système est équivalent à :
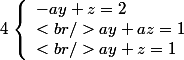
Et à :
=0<br />\end{array}\right)
Etude de cas :
1) a=1 alors le système à pour p-uplets (3-2z, 1-z, z)
2) a différent de 1 alors on a :
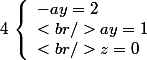
3) a différent de 0 alors pas de solution.
4) a différent de 0 et 1 alors le système a un unique p-uplet (3, 1/a, 0).
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 25 Oct 2009, 22:09
par Timothé Lefebvre » 25 Oct 2009, 22:09
Timothé Lefebvre a écrit:Énoncé 1 (trigo) :Mq

on a

et que

on a

Correction :
1) f(x)=x-sin(x). Définie sur R+ et la dérivée première de f est positive, de plus on a f(0)=0 d'où f est positive.
2)
=cos(-1+\frac{x^2}{2})
. Définie sur R. Sa dérivée première en 0 telle que g'(0) vaut g(0) qui vaut 0. De plus, sa dérivée seconde est supérieure à 0.
On pose le tableau de signes de g' puis le tableau de variations de g et on remarque que celle-ci est positive.
-
Billball
- Membre Complexe
- Messages: 2669
- Enregistré le: 31 Mar 2006, 19:13
-
 par Billball » 25 Oct 2009, 22:50
par Billball » 25 Oct 2009, 22:50
(ps : quand tu mets une équation cubique, pas de racine réelle, sinon c'est "bidon" enfin ca demande aucune réflexion :--: )
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 26 Oct 2009, 07:41
par Timothé Lefebvre » 26 Oct 2009, 07:41
Encore faut-il la trouver ;)
Bon évidemment si on la considère comme évidente aux vues des coeff du polynômes ça devient niveau basique mais bon. Pour des élèves qui n'en ont jamais rencontré c'est jouable !
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 26 Oct 2009, 10:07
par Timothé Lefebvre » 26 Oct 2009, 10:07
Timothé Lefebvre a écrit:Énoncé 7 (système) :Résoudre le système d'inconnue a et b tq
 \in \mathbb{C}^2)
:
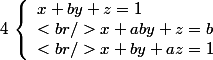
Correction :
On procède par équivalences :
y+(1-a^2)z=1-a\\<br />b(a-1)y+(1-a)z=b-1<br />\end{array}<br />\right \Leftrightarrow<br /><br />\rm \left\{<br />\begin{array}<br />x+by+az=1\\<br />b(1-a)y+(1-a^2)z=1-a\\<br />(1-a)(2+a)z=b-a<br />\end{array}<br />\right)
Ici on doit faire une étude de cas sur a et b :
1) Si a =1 alors
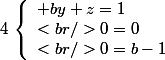
2) Si b différent de 1 alors il n'y a pas de solution.
3) Si b=1 alors x+y+z=1.
4) Si a=-2 alors
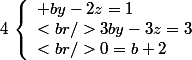
5) Si b différent de -2 alors il n'y a pas non plus de solution.
6) Si b=-2 alors

7) Si b=0 alors il n'y a encore pas de solution.
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 26 Oct 2009, 10:11
par Timothé Lefebvre » 26 Oct 2009, 10:11
Pour ceux que ça intéresse je modifie mon post initial en y ajoutant les différents exos traités dans ce topic.
J'apporterai la correction du huitième d'ici ce soir.
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 26 Oct 2009, 10:15
par Zweig » 26 Oct 2009, 10:15
Bug d'affichage pour mon système. Je réitère :
Résoudre dans
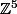
le système suivant :
[CENTER]

[/CENTER]
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 26 Oct 2009, 11:31
par benekire2 » 26 Oct 2009, 11:31
Zweig a écrit:Bug d'affichage pour mon système. Je réitère :
Résoudre dans
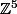
le système suivant :
[CENTER]

[/CENTER]

Donne nous des pistes stp
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 27 Oct 2009, 15:13
par Timothé Lefebvre » 27 Oct 2009, 15:13
Timothé Lefebvre a écrit:Énoncé 8 (système et paramètre) :Pareil, dans

et de paramètre m :
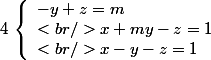
Correction :
Si m=1 alors S={(y, y, -1)} avec y dans C.
Si m différent de 1 alors S = {(m+(-)1)/2,0}
Simple

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 51 invités
et de paramètre a tq
:

on a
et que
on a
:



 [/CENTER]
[/CENTER]