Preuve de l'inégalité de Jordan avec des outils niveau lycée

[Olympus]

Bonjour !

Bon voilà, certes cette inégalité sort du programme du lycée, mais je suis quand même intéressé par une preuve ne faisant pas intervenir les intégrales, ni les dérivées ( pas encore vues en classe ) .

Un petit rappel de l'inégalité :

.

J'ai suivi la même méthode que celle présentée sur plusieurs sites comme : http://jwilson.coe.uga.edu/EMT725/Jordan/Jordan.html .

Mais le problème c'est : comment montrer alors que la courbe la plus courte entre deux points est un segment ? Plus précisément, comment montrer que la longueur PQ est inférieure à celle de l'arc PAQ ?

Est-ce possible de démontrer cela rien qu'avec des outils élémentaires ?

Merci !

[Ericovitchi]

C'est un axiome de la géométrie Euclidienne que le plus court chemin entre deux points est la ligne droite. Et si tu n'admets pas cet axiome, tu n'es pas en géométrie euclidienne (Et ça existe, il y a des géométries elliptiques, hyperboliques, ... ).
Mais là tu es dans un plan, donc tu dois admettre cet axiome.

[Olympus]

C'est un axiome de la géométrie Euclidienne que le plus court chemin entre deux points est la ligne droite. Et si tu n'admets pas cet axiome, tu n'es pas en géométrie euclidienne (Et ça existe, il y a des géométries elliptiques, hyperboliques, ... ).
Mais là tu es dans un plan, donc tu dois admettre cet axiome.

Ben ce qui est bizarre alors, c'est que c'est mon prof qui m'a demandé de démontrer cela ...

[beagle]

Une courbe versus segment.
on peut diviser la courbe en plus petits éléments tels que:
un point sur la courbe forme un triangle avec le segment.
Le plus court chemin est un seul coté de triangle plus petit que la somme de deux cotés de triangles.
Et encore, le point pris sur la courbe délimite deux courbes qui sont elles-mèmes plus longues que l'un des cotés du triangle pour la mème raison,
et c'est infiniment redécoupable en éléments plus grands.

faut redécouper parce que la courbe peut passer d'un coté à l'autre de ton segment

pour l'arc versus la corde, il n' y a pas à rediviser la courbe, je n'avais pas tout lu.
De tout point de l'arc tu peux faire passer une perpendiculaire à la corde, cela forme deux triangles rectangles, ou un triangle rectangle et sa hauteur,
ou bien les deux mèmes triangles rectangles si on est au milieu.
bref la longueur sur la corde est plus petite que l'hypoténuse des triangles rectangles.
Ensuite l'hypoténuse est une nouvelle corde qui délimite un nouvel arc de cercle et c'est idem, toujour plus petit sur corde que les hypoténuses qui délimitent de nouveaux arcs etc...

[Olympus]

Une courbe versus segment.
on peut diviser la courbe en plus petits éléments tels que:
un point sur la courbe forme un triangle avec le segment.
Le plus court chemin est un seul coté de triangle plus petit que la somme de deux cotés de triangles.
Et encore, le point pris sur la courbe délimite deux courbes qui sont elles-mèmes plus longues que l'un des cotés du triangle pour la mème raison,
et c'est infiniment redécoupable en éléments plus grands.

faut redécouper parce que la courbe peut passer d'un coté à l'autre de ton segment

pour l'arc versus la corde, il n' y a pas à rediviser la courbe, je n'avais pas tout lu.
De tout point de l'arc tu peux faire passer une perpendiculaire à la corde, cela forme deux triangles rectangles, ou un triangle rectangle et sa hauteur,
ou bien les deux mèmes triangles rectangles si on est au milieu.
bref la longueur sur la corde est plus petite que l'hypoténuse des triangles rectangles.
Ensuite l'hypoténuse est une nouvelle corde qui délimite un nouvel arc de cercle et c'est idem, toujour plus petit sur corde que les hypoténuses qui délimitent de nouveaux arcs etc...

Je ne sais pas si j'ai bien compris, mais à chaque division, on est confronté au problème arc vs. segment . Je ne sais pas aussi ce que ça donne si on continue à diviser jusqu'à l'infini ...

Certes, plus on avance dans les divisions, plus on se rapproche de l'arc, or c'est juste ça, une approximation de l'arc .

On peut aussi faire à peu près la même chose, sauf qu'on va prendre n'importe quel point M de l'arc, ce qui nous donnerait un triangle ( pas nécessairement rectangle ), et selon l'inégalité triangulaire, on aura , ensuite, on voit que M divise l'arc en deux parties, donc on va refaire la même chose et prendre un autre point de l'arc AM etc... et cela jusqu'à l'infini .

[beagle]

oui, c'est cela , j'ai rédigé rapidos,
et pour la première partie je n'avais pas regardé le problème avec un arc,
donc il fallait faire cela pour toute courbe, y compris biscornue, sinusoidale, etc ..., donc fallait redécouper d'abord.

Oui, soit un triangle tout seul,
soit avec les deux triangles.

Cela ne pose pas de soucis d'aller vers l'infini puisque à chaque étape tu as plus de longeur,
donc la corde de départ est plus petite que les segments de triangles,
qui sont eux aussi des cordes plus petits que,
plus petits que
plus petits que
cela ne pourra jamais ètre inversé,...

[Olympus]

D'accord, ce sera donc ce que je présenterai au prof Lundi prochain ( même si, comme je connais bien le prof, j'aurais droit à un "mais c'est plus intuitif que mathématique !" ) .

Je réfléchirai encore un peu plus dessus ce soir ( je verrais si ça ne donnerait pas une version plus acceptable du raisonnement en employant les suites ) .

Merci à tous :-)

[beagle]

oui, t'as raison c'est pas très présentable.
j'ai vu le titre, j'ai essayé avec des outils basiques,
ce sont des outils de collège.
t'es au lycée, cela doit se présenter mieux.
Avec les suites, possible, c'est loin pour moi.
Avec la récurrence?Je sais pas si on peut le reformuler et le récurrer.
Bon, t'auras de l'aide d'autres membres du forum.
Remonte le fil si c'est pas le cas.

[Olympus]

Pour les suites c'est juste une idée . En effet, j'ai vu que la plupart des constructions géométriques faisant intervenir des répétitions de la même action "n" fois ( fractales etc... ) peuvent se traduire sous forme de suites . Donc ce serait possible de traduire aussi ces divisions en suites . C'est assez vague car j'ai pas encore trop réfléchi dessus, en fait je verrais ce que ça donnerait, par exemple démontrer avec l'inégalité triangulaire que 2U(n) > U(n-1), ensuite utiliser la récurrence + pythagore etc... et tomber sur .

Ensuite, j'ajouterai un petit truc intuitif comme : quand n tend vers +inf, se rapproche de la longueur de l'arc .

[Olympus]

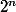
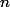
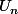
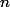
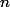
Effectivement ça marche et c'est plus clean en prouvant que ( étant le nombre des segments à la division , et étant la longueur de chaque segment à cette même division ) . Ensuite, plus est grande ( en gros, quand tend vers l'infini ), plus la nouvelle courbe constituée des petits segments se rapproche de l'arc . 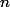La nouvelle courbe étant plus longue que AB ( selon ), l'arc le sera aussi vu que leurs longueurs sont très proches quand tend vers l'infini .

Maintenant j'ai un autre problème .

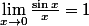
En effet, si je voulais démontrer l'inégalité de Jordan, c'était pour montrer que , sans recourir aux dérivées .

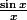
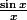
En effet, mon idée était d'encadrer entre deux expressions dont les limites seraient 1 ( et donc selon le théorème des gendarmes, la limite de serait aussi 1 ) .

Donc pour l'instant, avec l'inégalité de Jordan, j'ai : .

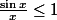
L'autre côté de l'inégalité ne m'intéresse pas vu qu'il ne me donne pas ce que je veux .

En cherchant un peu, je suis tombé sur une revue chinoise où l'inégalité de Jordan a été réécrite dans une forme plus précise : .

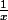
C'est le côté gauche de l'inégalité qui m'intéresse, car si on le multiplie par , sa limite quand x tend vers 0 devient 1 .

Mais dans la revue en question, il l'ont démontré en employant la dérivée + Hôpital, donc pas vraiment une preuve niveau lycée .

Vous en pensez quoi ? Cela vaut-il la peine de se casser la tête pour cette dernière inégalité ?

[benekire2]

ben pour la limite de sinx/x en 0 ( je crois que c'est ce que tu veut montrer )
montre d'abord que sur 0 ; pi/2 :



et tu devrais conclure divisant par sinx et en inversant ( et par parité étendre a l'intervalle -pi/2 ; 0)

[Olympus]

ben pour la limite de sinx/x en 0 ( je crois que c'est ce que tu veut montrer )
montre d'abord que sur 0 ; pi/2 :



et tu devrais conclure divisant par sinx et en inversant ( et par parité étendre a l'intervalle -pi/2 ; 0)

Génial !

Pour , déjà démontré . Plus qu'à démontrer que ( j'ai fait exprès de réécrire comme ça, car il suffirait de montrer que l'arc de longueur est plus petit que le segment de longueur ) .

Merci !

[benekire2]

de rien , tu pourra me montrer ta démo complète ? Merci.

[Olympus]

de rien , tu pourra me montrer ta démo complète ? Merci.

Pas de problème, si j'y arrive bien sûr :we:

[Olympus]

Grrrr encore une fois confronté à un nouveau problème de segment ( de longueur ) vs arc ( ) ... Je devrais y arriver une nouvelle fois avec une approximation de l'arc mais bon la flemme, car c'est pas évident de démontrer que la longueur de chaque petit segment à la division est plus petit que , étant le segment de longueur sur le cercle trigonométrique . Mais une fois cela fait, il suffit de dire que quand tend vers l'infini, la somme des longueurs des petits segments se rapproche de la longueur de l'arc ( et donc ) .

Quelqu'un n'aurait pas une meilleure approche ?

PS : la méthode que j'emploie pour donner une approximation de l'arc s'appelle la méthode d'exhaustion .

[Ben314]

Salut,
Si ça t'interesse et que tu veux pas trop t'emm... avec le problème de savoir si un arc est plus grand qu'un segment, raisonne avec des surface :

Tu prend M sur le cercle trigo qui correspond à un x de ]0,pi/2[ et tu considère les trois portions du plan :
1) le triangle (OMA) où A est le point (1,0)
2) la "portion de camembert" délimité par l'axe des x, la droite (OM) et le cercle trigo
3) le triangle (OKA) ou K est l'intersection de (OM) avec la tangente d'équation x=1 et A est le point (1,0)

Ces ensembles sont clairement contenus les uns dans les autres.
Quelles sont leurs surfaces respectives ?
(pour la surface de la "portion de camemembert", tu fait une règle de trois en partant du fait que la surface totale du disque est pi.R²=pi car R=1)