Une équation réciproque
51 messages
- Page 1 sur 3 - 1, 2, 3
Equation réciproque
Bonsoir les gens
L'équation : 10x^4-77x^3+150x²-77x+10=0
a)0 ne peut être la solution car le résultat sera de 10 (est-ce que je dois préciser pourquoi?)
b)démontrer que x est une solution si et seulement si 1/x est une solution
Et je ne sais pas quoi faire... merci de votre aide
L'équation : 10x^4-77x^3+150x²-77x+10=0
a)0 ne peut être la solution car le résultat sera de 10 (est-ce que je dois préciser pourquoi?)
b)démontrer que x est une solution si et seulement si 1/x est une solution
Et je ne sais pas quoi faire... merci de votre aide
Proriko a écrit:Bonsoir les gens
L'équation : 10x^4-77x^3+150x²-77x+10=0
a)0 ne peut être la solution car le résultat sera de 10 (est-ce que je dois préciser pourquoi?)
b)démontrer que x est une solution si et seulement si 1/x est une solution
Et je ne sais pas quoi faire... merci de votre aide
Tu remplaces "0 ne peut être la solution car le résultat sera de 10"
par "0 ne peut être la solution car si on remplace x par 10 on n'obtient pas 0"
Tu sais donc que tu peux essayer la solution X = 1/x
Tu obtiendras une équation équivalente puisque x = 0 n'est pas solution de l'équation initiale
Si f
Proriko a écrit:Je n'ai pas vraiment compris pourquoi X=1/x peut être solution
Sinon f1}{x})1/x) = 10*1/x^4 - 77*1/x^3 + 150*1/x² - 77*1/x + 10
Puisque x = 0 n'est pas solution de f(x) =0, il y a équivalence entre f(1/x) = 0 et f(x) =0
ou comme le dit l'énoncé : "x est une solution si et seulement si 1/x est une solution"
Proriko a écrit:Je suis un peu perdu...
J'ai très bien compris : f(1/x)=10/x^4 - 77/x^3 + 150/x² - 77/x + 10
x^4 f(1/x) = 10 -77x +150 x^2 -77x^3 + 10x^4 = f(x)
mais pourquoi dois t-on utilisé x^4 ?
Par contre, en divisant l'équation de départ par x^2 et en regroupant certains termes de manière adéquate, on obtient
P(x)=(10x^4 - 77x^3 + 150/x² - 77 + 10)/x^2= [10(x^2 + 1/x^2)-77 (x+1/x) +150]/x^2
soit l'équation 10(x^2 + 1/x^2)-77 (x+1/x) +150=0
Il ne te reste plus qu'a exprimer x^2+1/x^2 en fonction de x+1/x et d'écrire l'équation du second degré en u = x+1/x
Proriko a écrit:Doucement ! :O Je n'ai absolument rien compris car je suis totalement perdu !
J'ai dis avoir compris que f(1/x)=10/x^4 - 77/x^3 + 150/x² - 77/x + 10 et qu'ainsi en divisant x^4 on obtient 10 -77x +150 x^2 -77x^3 + 10x^4 = f(x)
Mais pourquoi doit t-on divisé par x^4?
C'était une fausse piste, donc à laisser tomber !
La division par x^2 va te permettre de faire apparaître une équation du second degré d'inconnue u = x+1/x
et ça on sait la résoudre
il y a deux aspects bien distincts (mais liés)
i) si est solution, alors
est solution, alors  est solution
est solution
(ça se montre en divisant l'équation par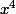 )
)
ii) on divise par et on pose
et on pose 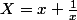
le degré de l'équation en est le double du degré de l'équation en
est le double du degré de l'équation en 
(ça se montre en divisant l'équation par )
)
maintenant, si tu trouves par exemple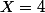 comme solution,
comme solution,
tu dois ensuite résoudre
i) si
(ça se montre en divisant l'équation par
ii) on divise par
le degré de l'équation en
(ça se montre en divisant l'équation par
maintenant, si tu trouves par exemple
tu dois ensuite résoudre
Une équation réciproque
Bonjour les gens , j'ai un DM que j'ai commencé et j'ai déjà reçu un peu d'aide mais je suis encore galère donc je m'adresse à vous .
L'équation : 10x^4-77x^3+150x²-77x+10=0
a)0 ne peut être la solution car le résultat sera de 10 (est-ce que je dois préciser pourquoi?)
b)démontrer que x est une solution si et seulement si 1/x est une solution
au lieu de faire f(x) on fait f(1/x) ce qui donne 10*1/x^4 - 77*1/x^3 + 150*1/x² - 77*1/x + 10
Si f(x)=0 alors f(1/x) aussi égal à 0 normalement?
Comment le montrer?
Merci de votre aide
L'équation : 10x^4-77x^3+150x²-77x+10=0
a)0 ne peut être la solution car le résultat sera de 10 (est-ce que je dois préciser pourquoi?)
b)démontrer que x est une solution si et seulement si 1/x est une solution
au lieu de faire f(x) on fait f(1/x) ce qui donne 10*1/x^4 - 77*1/x^3 + 150*1/x² - 77*1/x + 10
Si f(x)=0 alors f(1/x) aussi égal à 0 normalement?
Comment le montrer?
Merci de votre aide
Salut !
Posons=10x^4-77x^3+150x^2-77x+10) .
.
a) Si était solution de
était solution de =0) , alors on aurait
, alors on aurait =0) .
.
Or=10) donc c'est impossible.
donc c'est impossible.
b) Si est solution alors
est solution alors =0) .
.
Pour montrer alors que = 0) , il suffit de diviser
, il suffit de diviser ) par
par 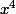 :++:
:++:
Proriko a écrit:Bonjour les gens , j'ai un DM que j'ai commencé et j'ai déjà reçu un peu d'aide mais je suis encore galère donc je m'adresse à vous .
L'équation : 10x^4-77x^3+150x²-77x+10=0
a)0 ne peut être la solution car le résultat sera de 10 (est-ce que je dois préciser pourquoi?)
b)démontrer que x est une solution si et seulement si 1/x est une solution
au lieu de faire f(x) on fait f(1/x) ce qui donne 10*1/x^4 - 77*1/x^3 + 150*1/x² - 77*1/x + 10
Si f(x)=0 alors f(1/x) aussi égal à 0 normalement?
Comment le montrer?
Merci de votre aide
Posons
a) Si
Or
b) Si
Pour montrer alors que
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Proriko a écrit:Bonjour les gens , j'ai un DM que j'ai commencé et j'ai déjà reçu un peu d'aide mais je suis encore galère donc je m'adresse à vous .
L'équation : 10x^4-77x^3+150x²-77x+10=0
a)0 ne peut être la solution car le résultat sera de 10 (est-ce que je dois préciser pourquoi?)
b)démontrer que x est une solution si et seulement si 1/x est une solution
au lieu de faire f(x) on fait f(1/x) ce qui donne 10*1/x^4 - 77*1/x^3 + 150*1/x² - 77*1/x + 10
Si f(x)=0 alors f(1/x) aussi égal à 0 normalement?
Comment le montrer?
Merci de votre aide
Pourquoi ouvres-tu un nouveau fil sur ce problème alors que plusieurs personnes t'ont déjà répondu.
Voir : http://www.maths-forum.com/equation-reciproque-146289.php
Si tu ne comprends pas une réponse précise-le dans le premier fil ouvert.
As-tu seulement lu la charte du forum ?
51 messages
- Page 1 sur 3 - 1, 2, 3
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 144 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
