Bonjour, j'ai un exercice sur les logarithmes, où je dois déterminer le nombre de solutions d'une équation sans calculatrice. L'équation en question est : (ln(x))^3 = x
Je sais que sur ]0;1[, il n'y a pas de solution, mais je n'arrive pas à trouver pour [1;+infini[
J'ai déterminé la dérivée de (ln(x))^3-x qui est : (3(ln(x))^2-1)/x
Et est aussi transformé ln(x) en log(x), mais je n'arrive pas à étudier le signe de cette dérivée ou à trouver les solutions.
Si vous pouviez m'aider j'en serais ravi, merci.
Terminale S Logarithme Déterminer le nombre de solutions
4 messages
- Page 1 sur 1
Re: Terminale S Logarithme Déterminer le nombre de solutions
TorVik07 a écrit:Bonjour, j'ai un exercice sur les logarithmes, où je dois déterminer le nombre de solutions d'une équation sans calculatrice. L'équation en question est : (ln(x))^3 = x
Je sais que sur ]0;1[, il n'y a pas de solution, mais je n'arrive pas à trouver pour [1;+infini[
J'ai déterminé la dérivée de (ln(x))^3-x qui est : (3(ln(x))^2-1)/x
Je ne suis pas d'accord avec ta dérivée.
Re: Terminale S Logarithme Déterminer le nombre de solutions
Salut,
A mon avis, surtout si tu doit tout faire sans machine, c'est plus que pas con de poser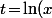) de façon à ce que l'équation à résoudre soit
de façon à ce que l'équation à résoudre soit 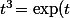) .
.
Ensuite, si on pose\!=\exp(t)\!-t^3) on peut (avec le calcul des dérivées seconde et troisième) dresser les variations de la fonction
on peut (avec le calcul des dérivées seconde et troisième) dresser les variations de la fonction  et trouver le nombre de solutions de l'équation
et trouver le nombre de solutions de l'équation \!=\!0) .
.
A mon avis, surtout si tu doit tout faire sans machine, c'est plus que pas con de poser
Ensuite, si on pose
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Terminale S Logarithme Déterminer le nombre de solutions
Oui, je me suis trompé en la tapant je voulais mettre : (3(ln(x))^2-x)/x
Et j'ai posé t=ln(x), et j'obtiens à la fin comme dérivée f'(t)=exp(t)-3t^2, cependant je n'arrive pas à étudier le signe de cette dérivée.
Merci beaucoup pour vos conseils
Et j'ai posé t=ln(x), et j'obtiens à la fin comme dérivée f'(t)=exp(t)-3t^2, cependant je n'arrive pas à étudier le signe de cette dérivée.
Merci beaucoup pour vos conseils
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 86 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
