[TS] Suites.
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 14 Nov 2010, 18:40
par Sa Majesté » 14 Nov 2010, 18:40
Oui
Mais encore une fois : "décroissante pour tout n", ça ne veut rien dire
-
Deluxor
- Membre Rationnel
- Messages: 581
- Enregistré le: 29 Oct 2007, 12:00
-
 par Deluxor » 14 Nov 2010, 18:45
par Deluxor » 14 Nov 2010, 18:45
On dit seulement :

pour tout

, donc la suite
)
est décroissante ?

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 14 Nov 2010, 18:46
par Sa Majesté » 14 Nov 2010, 18:46
Oui c'est ça
-
Deluxor
- Membre Rationnel
- Messages: 581
- Enregistré le: 29 Oct 2007, 12:00
-
 par Deluxor » 14 Nov 2010, 18:53
par Deluxor » 14 Nov 2010, 18:53
D'accord.
J'arrive maintenant à la 6)a. :
J'ai montré que
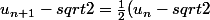+\frac{1}{u_n}-\frac{1}{sqrt{2}})
pour tout

.
Il faut maintenant déduire que
)
.
On sait que :

est négatif pour tout

. Mais je ne vois pas comment poursuivre...

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 14 Nov 2010, 18:57
par Sa Majesté » 14 Nov 2010, 18:57
Le problème c'est que tu ne réfléchis pas assez :hum:
Ici c'est tellement évident que je ne peux même pas te donner d'indice sans te donner la solution
-
Deluxor
- Membre Rationnel
- Messages: 581
- Enregistré le: 29 Oct 2007, 12:00
-
 par Deluxor » 14 Nov 2010, 19:04
par Deluxor » 14 Nov 2010, 19:04
D'un côté on a :

De l'autre on a :
 \geq 0)
On ne peut pas additionner membre à membre vu qu'il n'y a pas le même sens. Donc je bloque.

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 14 Nov 2010, 19:15
par Sa Majesté » 14 Nov 2010, 19:15
Tu as tout écrit pourtant :marteau:
Deluxor a écrit:On sait que :

est négatif pour tout

.
Pour tout n,

Il n'y a plus qu'à additionner
)
des 2 côtés de l'inégalité pour obtenir
Pour tout n,
+\frac{1}{u_n}-\frac{1}{sqrt{2}} \leq \frac{1}{2}(u_n-sqrt{2}))
et comme
Deluxor a écrit:J'ai montré que
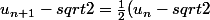+\frac{1}{u_n}-\frac{1}{sqrt{2}})
pour tout

.
on obtient pour tout n,
)
.
-
Deluxor
- Membre Rationnel
- Messages: 581
- Enregistré le: 29 Oct 2007, 12:00
-
 par Deluxor » 14 Nov 2010, 19:46
par Deluxor » 14 Nov 2010, 19:46
Compris !

J'en arrive au raisonnement par récurrence.
J'ai prouvé l'initialisation.
J'ai supposé que

et je veux prouver que

.
Je sais que
)
, je bloque encore... :/

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 14 Nov 2010, 20:02
par Sa Majesté » 14 Nov 2010, 20:02
N'oublie jamais qu'un énoncé a une structure
Parfois on te demande de démontrer qqch puis on te dit : en déduire que
Parfois on ne te dit rien mais la structure te donne une indication. Par ex ici tu en es à la question 6b. Et avant il y avait la question 6a. C'est qu'il doit y avoir un lien entre ces 2 questions ...
-
Deluxor
- Membre Rationnel
- Messages: 581
- Enregistré le: 29 Oct 2007, 12:00
-
 par Deluxor » 14 Nov 2010, 20:24
par Deluxor » 14 Nov 2010, 20:24
Ce lien, je l'ai trouvé, je l'ai mis plus haut. C'est la simplification nécessaire pour faire apparaître une expression de la forme

qui pose problème.

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 14 Nov 2010, 20:43
par Sa Majesté » 14 Nov 2010, 20:43
Tu as
)
et

Tu veux prouver que

-
Deluxor
- Membre Rationnel
- Messages: 581
- Enregistré le: 29 Oct 2007, 12:00
-
 par Deluxor » 14 Nov 2010, 21:02
par Deluxor » 14 Nov 2010, 21:02
On part de l'hypothèse de récurrence :

 \leq 7 \times \frac{1}{2^{p+1}})
or,
)
Mais on n'est pas sur que :

, si ?

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 14 Nov 2010, 21:08
par Sa Majesté » 14 Nov 2010, 21:08
Laisse tomber la partie

, tu l'as déjà démontré au 4b)
-
Deluxor
- Membre Rationnel
- Messages: 581
- Enregistré le: 29 Oct 2007, 12:00
-
 par Deluxor » 14 Nov 2010, 21:12
par Deluxor » 14 Nov 2010, 21:12
Sa Majesté a écrit:Laisse tomber la partie

, tu l'as déjà démontré au 4b)
Sauf que là il s'agit de prouver

et non
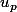

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 14 Nov 2010, 21:26
par Sa Majesté » 14 Nov 2010, 21:26
C'est pareil (ou presque)
Je croyais que c'était clair pourtant
Deluxor a écrit:J'ai donc seulement à dire que, comme pour tout

,

, alors pour tout

,

?
-
Deluxor
- Membre Rationnel
- Messages: 581
- Enregistré le: 29 Oct 2007, 12:00
-
 par Deluxor » 14 Nov 2010, 21:31
par Deluxor » 14 Nov 2010, 21:31
Je me mélange les pinceaux !
J'ai compris, merci.
La suite est donc bornée. Comment peut-on déduire la convergence ?

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 14 Nov 2010, 21:37
par Sa Majesté » 14 Nov 2010, 21:37
Le théorème des gendarmes
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités
