Suite définie par intégration
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
upium666
- Membre Relatif
- Messages: 404
- Enregistré le: 14 Mai 2012, 21:44
-
 par upium666 » 24 Juin 2013, 20:13
par upium666 » 24 Juin 2013, 20:13
Bonjour à tous et à toutes !
Cette année j'ai été en 1ère S, donc je n'ai pas le bagage nécessaire pour résoudre cet exercice seul mais je serais curieux d'en avoir le résultat préalablement démontré si possible :
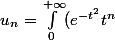 dt)
Expliciter la suite (=Exprimer la suite en fonction de n)
Merci !
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 24 Juin 2013, 20:50
par XENSECP » 24 Juin 2013, 20:50
Intégration par parties pour trouver une relation de récurrence sur Un ;)
-
Black Jack
 par Black Jack » 25 Juin 2013, 09:56
par Black Jack » 25 Juin 2013, 09:56
Par exemple IPP en :
Posant t.e^-t².dt = dv ----> v = -(1/2).e^-t²
et en posant t^(n-1) = u ---> du = (n-1).t^(n-2) dt
Cela devrait conduire à : U_(n) = ((n-1)/2).U_(n-2)
Duquel on tire immédiatement : U_(n+2) = ((n+1)/2).U_(n)
Comme U_(0) a un résultat qui devrait être connu ? et que U_(1) est facile à calculer ...
:zen:
-
upium666
- Membre Relatif
- Messages: 404
- Enregistré le: 14 Mai 2012, 21:44
-
 par upium666 » 26 Juin 2013, 10:04
par upium666 » 26 Juin 2013, 10:04
Black Jack a écrit:Par exemple IPP en :
Posant t.e^-t².dt = dv ----> v = -(1/2).e^-t²
et en posant t^(n-1) = u ---> du = (n-1).t^(n-2) dt
Cela devrait conduire à : U_(n) = ((n-1)/2).U_(n-2)
Duquel on tire immédiatement : U_(n+2) = ((n+1)/2).U_(n)
Comme U_(0) a un résultat qui devrait être connu ? et que U_(1) est facile à calculer ...
:zen:
Après ce sera une relation de récurrence (linéaire ?) d'ordre 2 qui nous permettra de trouver

?

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 26 Juin 2013, 19:34
par capitaine nuggets » 26 Juin 2013, 19:34
Salut !
)
vérifie
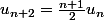
qui est une relation de récurrence non linéaire.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 61 invités
