Le mieux, c'est sûrement d'utiliser les intervalles

,
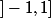
et
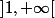
.
L'intérêt de les prendre comme ça est :
1. Ces trois intervalles recouvrent l'ensemble de définition,

donc il n'y a pas d'autre solution que celles qu'on trouve dans ces intervalles.
2. Comme ils sont disjoints, (ils ont une intersection vide ou ils ne se "coupent" pas, comme vous préférez), ça garantit qu'il y a exactement trois solutions et pas moins. En effet, si on prend par exemple

et
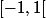
pour les deux premiers, alors on montre qu'il y a une unique solution dans

, qu'il y a une unique solution dans
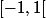
, mais ça dit seulement qu'il y a une ou deux solutions dans
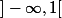
, car la solution sur chaque intervalle pourrait être -1. Il faudrait alors vérifier que ce n'est pas -1, ce qui fait du travail en plus.
Remarquez que j'aurais très bien pu choisir les intervalles
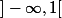
,
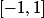
et
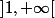
. Ce que j'ai dit marche pour tous les types de ces trois intervalles du moment qu'ils ne se rencontrent pas et que leur réunion est

.
Il faut tout de même faire attention à ce que f' soit bijective sur chacun de ces intervalles pour garantir l'unicité des solutions.
Voilà! :happy2:
