Recherche exercices arithmétique
Recherche exercices arithmétique
Bonjour,
J'ai décidé de prendre de l'avance sur mon futur programme et j'aimerais avoir des exercices d'arithmétique de niveau terminale (peu importe le ou les chapitres concernés) !
Donc si vous avez la possibilité de m'en proposer ce serait génial, merci d'avance ! :)
Bonne journée ! :lol3:
PS: Inutile de me donner le site internet XMaths puisque quelqu'un me l'a déjà donné, donc la quasi totalité des exercices ont déjà été faits ! (en réalité j'ai même appris mon cours dessus)
J'ai décidé de prendre de l'avance sur mon futur programme et j'aimerais avoir des exercices d'arithmétique de niveau terminale (peu importe le ou les chapitres concernés) !
Donc si vous avez la possibilité de m'en proposer ce serait génial, merci d'avance ! :)
Bonne journée ! :lol3:
PS: Inutile de me donner le site internet XMaths puisque quelqu'un me l'a déjà donné, donc la quasi totalité des exercices ont déjà été faits ! (en réalité j'ai même appris mon cours dessus)
Waax22951 a écrit:Bonjour,
J'ai décidé de prendre de l'avance sur mon futur programme et j'aimerais avoir des exercices d'arithmétique de niveau terminale (peu importe le ou les chapitres concernés) !
Donc si vous avez la possibilité de m'en proposer ce serait génial, merci d'avance !
Bonne journée ! :lol3:
PS: Inutile de me donner le site internet XMaths puisque quelqu'un me l'a déjà donné, donc la quasi totalité des exercices ont déjà été faits ! (en réalité j'ai même appris mon cours dessus)
Salut,
Voici un problème que je trouve sympa:
Soit f une fonction à valeurs dans N qui vérifie:
- f(mn)=f(n)+f(m)
- f(10)=0
- f(n)=0 si le chiffre des unités de n est 3
Montrer que f(n)=0 pour tout entier positif n.
Sinon en plus "classique" sur les congruences:
Déterminer les chiffres x,y tels que :
Et il y a quelques exos d'arithmétiques ici: http://mathsplus.net/ mais le site est vraiment laid (bien qu'à jour) et les formules ne s'affichent pas très bien.
Je suis d'ac avec t.itou, il est moche le site (a fortiori créé par des LLG donc il l'est encore plus).
Je me souviens d'un site marocain que j'avais utilisé à l'époque pour réviser mon bac. Vais essayer de le retrouver.
Voilà, l'ai retrouvé
http://www.mathsland.com/
Je me souviens d'un site marocain que j'avais utilisé à l'époque pour réviser mon bac. Vais essayer de le retrouver.
Voilà, l'ai retrouvé
http://www.mathsland.com/
Merci pour toutes ces réponses ! :lol3:
C'est vrai que mathsplus n'est vraiment pas beau, mais je regarderai les exercices quand même, tout comme sur mathsland ! :lol3:
J'ai deux questions t.itou29:
La première est sur l'exercice sur les fonctions dans : J'ai réussi à déduire quelques propriétés évidentes de f mais je ne vois pas comment on fait pour obtenir f(p) avec p un nombre premier.. Fais-je faute route ?(je n'ai jamais fait d'exercice dans ce style alors il me faut plus de temps pour réfléchir..).
: J'ai réussi à déduire quelques propriétés évidentes de f mais je ne vois pas comment on fait pour obtenir f(p) avec p un nombre premier.. Fais-je faute route ?(je n'ai jamais fait d'exercice dans ce style alors il me faut plus de temps pour réfléchir..).
Le seconde concerne l'autre exercice: je n'ai trouvé cette notation qu'une seule fois, donc j'aimerais être sûr de ne pas me tromper (j'avais trouvé un résultat mais il se trouve être faut, donc je pense que ma compréhension n'est pas bonne..)
Par définition, on a:
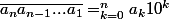
Est-ce bien ça ?
Si c'est le cas, on a bien:
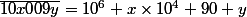
Est-ce ça ? :hein:
PS: En fait je viens de trouver:
;(1,7);(2,6);(3,5);(4,4);(5,3);(6,2);(7,1);(8,0)})
C'est bon là ? ^^
C'est vrai que mathsplus n'est vraiment pas beau, mais je regarderai les exercices quand même, tout comme sur mathsland ! :lol3:
J'ai deux questions t.itou29:
La première est sur l'exercice sur les fonctions dans
Le seconde concerne l'autre exercice: je n'ai trouvé cette notation qu'une seule fois, donc j'aimerais être sûr de ne pas me tromper (j'avais trouvé un résultat mais il se trouve être faut, donc je pense que ma compréhension n'est pas bonne..)
Par définition, on a:
Est-ce bien ça ?
Si c'est le cas, on a bien:
Est-ce ça ? :hein:
PS: En fait je viens de trouver:
C'est bon là ? ^^
Waax22951 a écrit:Merci pour toutes ces réponses ! :lol3:
C'est vrai que mathsplus n'est vraiment pas beau, mais je regarderai les exercices quand même, tout comme sur mathsland ! :lol3:
J'ai deux questions t.itou29:
La première est sur l'exercice sur les fonctions dans: J'ai réussi à déduire quelques propriétés évidentes de f mais je ne vois pas comment on fait pour obtenir f(p) avec p un nombre premier.. Fais-je faute route ?(je n'ai jamais fait d'exercice dans ce style alors il me faut plus de temps pour réfléchir..).
Le seconde concerne l'autre exercice: je n'ai trouvé cette notation qu'une seule fois, donc j'aimerais être sûr de ne pas me tromper (j'avais trouvé un résultat mais il se trouve être faut, donc je pense que ma compréhension n'est pas bonne..)
Par définition, on a:
Est-ce bien ça ?
Si c'est le cas, on a bien:
Est-ce ça ? :hein:
f(mn)=f(m)+f(n) ça te rappelle quelle fonction ?
On note
Waax22951 a écrit:Merci pour toutes ces réponses ! :lol3:
C'est vrai que mathsplus n'est vraiment pas beau, mais je regarderai les exercices quand même, tout comme sur mathsland ! :lol3:
J'ai deux questions t.itou29:
La première est sur l'exercice sur les fonctions dans: J'ai réussi à déduire quelques propriétés évidentes de f mais je ne vois pas comment on fait pour obtenir f(p) avec p un nombre premier.. Fais-je faute route ?(je n'ai jamais fait d'exercice dans ce style alors il me faut plus de temps pour réfléchir..).
Le seconde concerne l'autre exercice: je n'ai trouvé cette notation qu'une seule fois, donc j'aimerais être sûr de ne pas me tromper (j'avais trouvé un résultat mais il se trouve être faut, donc je pense que ma compréhension n'est pas bonne..)
Par définition, on a:
Est-ce bien ça ?
Si c'est le cas, on a bien:
Est-ce ça ? :hein:
Pour le premier exercice tu peux t'intéresser aux chiffres des unités possibles pour un nombre premier >2 (il est assez original comme problème !)
Quant aux second c'est bien la bonne définition et tu peux "simplifier" (chercher à combien est congru 10^6+90 et 10^4x) l'expression de droite pour faciliter la recherche de des solutions
Sake a écrit:f(mn)=f(m)+f(n) ça te rappelle quelle fonction ?
On note
Ah oui en effet un légère erreur de ma part, merci de me la relever, je vais la corriger de ce pas !
Ça me fait penser à pas mal de fonction, le logarithme, l'exponentielle, et toutes les fonctions du même style..
Pour l'instant j'en ai déduit que
avec
Et
On a alors
Il suffit donc de démontrer que pour tout nombre premier p, f(p)=0..
J'ai bon ? :hein:
Waax22951 a écrit:Ah oui en effet un légère erreur de ma part, merci de me la relever, je vais la corriger de ce pas !
Ça me fait penser à pas mal de fonction, le logarithme, l'exponentielle, et toutes les fonctions du même style..
Pour l'instant j'en ai déduit que, que
, et que
.. Du coup, si on décompose n en facteurs premiers, on a:
avec
Et,
On a alors
Il suffit donc de démontrer que pour tout nombre premier p, f(p)=0..
J'ai bon ? :hein:
Oui c'est tout à fait ça ! :lol3:
(à la place de somme de p_i^alpha c'est alpha*f(p_i) mais ça doit etre un erreur de recopiage)
salut
f(mn) = f(m) + f(n) implique que f est croissante (puisqu'on travaille dans N)
or f(0) = f(10) = 0 dont f est nulle sur les 11 premiers entiers ... donc en particulier f(2) = 0
or = mf(2) = 0) pour tout m
pour tout m
et puisque f est croissante f est nulle pour tout k =< 2^m pour tout m
donc f est nulle
....
et il n'est même pas besoin de la troisième hypothèse ....
:lol3:
f(mn) = f(m) + f(n) implique que f est croissante (puisqu'on travaille dans N)
or f(0) = f(10) = 0 dont f est nulle sur les 11 premiers entiers ... donc en particulier f(2) = 0
or
et puisque f est croissante f est nulle pour tout k =< 2^m pour tout m
donc f est nulle
....
et il n'est même pas besoin de la troisième hypothèse ....
:lol3:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
zygomatique a écrit:salut
f(mn) = f(m) + f(n) implique que f est croissante (puisqu'on travaille dans N)
or f(0) = f(10) = 0 dont f est nulle sur les 11 premiers entiers ... donc en particulier f(2) = 0
orpour tout m
et puisque f est croissante f est nulle pour tout k =< 2^m pour tout m
donc f est nulle
....
et il n'est même pas besoin de la troisième hypothèse ....
:lol3:
Juste une question, comment montres-tu que f est croissante "proprement" (même croissante tout court) ?
zygomatique a écrit:f(mn) = f(m) + f(n) ==> f(mn) >= f(m) et f(mn) >= f(n) or puisque mn >= m et mn >= n on en déduit que f est croissante ....
parce que f est à valeur dans N donc positive ...
Je comprend toujours pas, pour montrer que f est croissante il faut montrer que f(n+1)>f(n). mn>=m -> f(mn)>=f(m) ne montre en rien (selon moi) que f est croissante.
Désolé si quelque chose d'évident m'échappe ..
On a f(8)>=f(4) mais rien ne dit (en se contentant des deux premières conditions) que f(8)>=f(7)...
J'approche du but !!
Je n'ai plus qu'à démontrer que si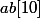 , alors
, alors =f(b)) ..!
..!
J'ai réussi pour quelques cas particuliers comme par exemple 15 et 5 ou même pour tous les nombres ayant 3 pour unité.. Du coup ça revient à démontrer que pour tout entiers et
et 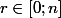 ,
, =f(r)) ..
..
En effet, si on a=f(r)) , on en déduit que pour tout nombre premier,
, on en déduit que pour tout nombre premier, 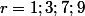 .
.
On a immédiatement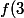=0) . Donc si
. Donc si  , alors
, alors 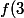=f(r)=0) .
.
On a aussi=2f(3)=0) . Donc si
. Donc si 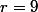 , alors
, alors =f(r)=0) .
.
On a=f(3)+f(7) \Leftrightarrow f(7)=0) . Donc si
. Donc si 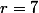 , alors
, alors =f(r)=0) .
.
On a finalement=f(21)=0) . Donc si
. Donc si 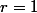 , alors
, alors =f(r)=0) .
.
Donc si p est premier, alors=0) . Puisque pour tout n,
. Puisque pour tout n, =\bigsum_{i=0}^k \alpha_i f(p_i)) avec
avec 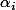 un entier naturel non nul et
un entier naturel non nul et  un nombre premier.
un nombre premier.
Puisque est premier,
est premier, =0) donc
donc =f(n)=0) pour tout entier naturel n.
pour tout entier naturel n.
Je crois avoir un début de démonstration mais je pense que la fatigue fait qu'il y a une énorme erreur de logique ou de calcul..:
f est une fonction à valeurs dans n, on en déduit donc que f est une fonction n'employant que les lois +, - et x.
On peut donc écrire que:
 \eq f(b) [10])
On a donc:
=10q+f(b)) avec
avec 
=10q'+f(a)) avec
avec 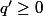
Donc=10q+f(b)=f(b)-10q' \Leftrightarrow 10q=-10q' \Leftrightarrow q=-q') .
.
Or et
et 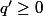 .
.
Donc q=q'=0.
On a finalement=f(b)+10q \Leftrightarrow f(a)=f(b)) .
.
Donc si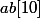 , alors
, alors =f(b)) .
.
Cette propriété permet donc d'affirmer que pour tout n, f(n)=0.
Si il y a une erreur, ne me donnez pas la solution, dites moi juste en quoi c'est faux !
Merci et bonne nuit ! :we:
Je n'ai plus qu'à démontrer que si
J'ai réussi pour quelques cas particuliers comme par exemple 15 et 5 ou même pour tous les nombres ayant 3 pour unité.. Du coup ça revient à démontrer que pour tout entiers
En effet, si on a
On a immédiatement
On a aussi
On a
On a finalement
Donc si p est premier, alors
Puisque
Je crois avoir un début de démonstration mais je pense que la fatigue fait qu'il y a une énorme erreur de logique ou de calcul..:
f est une fonction à valeurs dans n, on en déduit donc que f est une fonction n'employant que les lois +, - et x.
On peut donc écrire que:
On a donc:
Donc
Or
Donc q=q'=0.
On a finalement
Donc si
Cette propriété permet donc d'affirmer que pour tout n, f(n)=0.
Si il y a une erreur, ne me donnez pas la solution, dites moi juste en quoi c'est faux !
Merci et bonne nuit ! :we:
t.itou29 a écrit:Je comprend toujours pas, pour montrer que f est croissante il faut montrer que f(n+1)>f(n). mn>=m -> f(mn)>=f(m) ne montre en rien (selon moi) que f est croissante.
Désolé si quelque chose d'évident m'échappe ..
On a f(8)>=f(4) mais rien ne dit (en se contentant des deux premières conditions) que f(8)>=f(7)...
f est croissante ( a = f(a) = f(n) == 0
donc f(mn) >= f(n) et mn >= n
f(10) = f(2*5) = f(2) + f(5) = 0 ==> f(2) = f(5) = f(10) = 0
de même pour f(1) = f(1*1) et f(0) = f(0*0)
et les relations f(m^n) = mf(n) et [TEX]f(m^kn) = f(n) où m est un produit quelconque des entiers 2 et 5devraient permettre de conclure ...
il est vrai que ma démonstration manque de rigueur ...
et qu'il nous faut tout de même la troisième hypothèse ... soit f(10k + 3) = 0
ce qui permet immédiatement d'avoir f(k) = 0 pour tout k =< 10 hormis 7 ....
mais la démonstration de waax22951 est fausse ..
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
zygomatique a écrit:f est croissante ( a = f(a) = f(n) == 0
donc f(mn) >= f(n) et mn >= n
f(10) = f(2*5) = f(2) + f(5) = 0 ==> f(2) = f(5) = f(10) = 0
de même pour f(1) = f(1*1) et f(0) = f(0*0)
et les relations f(m^n) = mf(n) et [TEX]f(m^kn) = f(n) où m est un produit quelconque des entiers 2 et 5devraient permettre de conclure ...
il est vrai que ma démonstration manque de rigueur ...
et qu'il nous faut tout de même la troisième hypothèse ... soit f(10k + 3) = 0
ce qui permet immédiatement d'avoir f(k) = 0 pour tout k =< 10 hormis 7 ....
mais la démonstration de waax22951 est fausse ..
Oui, le problème c'est qu'il faut montrer que c'est aussi vrai pour les nombres premiers qui ne peuvent pas être décomposé directement avec la première relation. Du coup, on est obligé d'utiliser les deux autres hypothèses pour montrer que pour tout nombre premier p, f(p)=0 et dans ce cas, on a montré que c'est vrai pour tout n.
Waax22951 a écrit:J'approche du but !!
Je n'ai plus qu'à démontrer que si, alors
..!
J'ai réussi pour quelques cas particuliers comme par exemple 15 et 5 ou même pour tous les nombres ayant 3 pour unité.. Du coup ça revient à démontrer que pour tout entierset
,
..
En effet, si on a, on en déduit que pour tout nombre premier,
.
On a immédiatement. Donc si
, alors
.
On a aussi. Donc si
, alors
.
On a. Donc si
, alors
.
On a finalement. Donc si
, alors
.
Donc si p est premier, alors. Puisque pour tout n,
avec
un entier naturel non nul et
un nombre premier.
Puisqueest premier,
donc
pour tout entier naturel n.
Je crois avoir un début de démonstration mais je pense que la fatigue fait qu'il y a une énorme erreur de logique ou de calcul..:
f est une fonction à valeurs dans n, on en déduit donc que f est une fonction n'employant que les lois +, - et x.
On peut donc écrire que:
On a donc:avec
avec
Donc.
Oret
.
Donc q=q'=0.
On a finalement.
Donc si, alors
.
Cette propriété permet donc d'affirmer que pour tout n, f(n)=0.
Si il y a une erreur, ne me donnez pas la solution, dites moi juste en quoi c'est faux !
Merci et bonne nuit ! :we:
Quand tu dis f est une fonction n'employant que les lois +,-* tu veux dire quoi ?
Comme l'a dit Zygomatique, j'ai pas l'impression que ce soit correct.
Il suffit juste de montrer que tout nombre finissant par 1,3,7,9 a une image nulle par f (et en montrant en plus que f(0)=f(1)=f(2)=f(3)=f(5)=0 cela signifie tous les nombres premiers).
(Et les solutions que tu as trouvées au second exercice sont correctes )
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 52 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
