Recherche exercices arithmétique

[Waax22951]

Je vais essayer de le démontrer par les congruences aussi alors..!
Mais alors cela veut dire que , non ? (puisque pour tout entier a, il existe un r compris entre 0 et n-1 tel que a est congru à r modulo n..) :hein:
Je ne suis pas sûr de ce que j'avance, mais je crois qu'on peut prouver que les expressions ne sont pas plus factorisables..:
On peut démontrer que si a et b sont premiers entre eux, alors ils ne sont pas factorisables. Or 5 et 6 sont premiers entre eux, donc et sont aussi premiers entre eux (5 et 6 n'ont aucun facteurs premiers en commun donc et n'en ont pas non plus).
Donc n'est pas factorisable. Or on a:

Or 5 et 3 sont premiers entre eux, tout comme 5 et 2, donc n'est pas factorisable.
On fait la même chose avec :

Or 5 et 7 sont premiers entre eux, tout comme 6 et 5, donc n'est pas factorisable. Donc p=2 ou p=3 ou p=5. 3 et 5 ne divisent pas (Car 6 et 7 ne sont pas multiples de 5 et 4 et 5 ne sont pas multiples de 3). Donc p=2.
Après on fait la démonstration au dessus.. (après l'erreur de calcul est toujours possible pour ce qui suit..)

[zygomatique]

non 5 et 7 sont premiers entre eux et 5 + 7 = 12 est factorisable ....

Z/3Z = {{3k}, {3k + 1}, {3k + 2}} est un ensemble d'ensemble dont l'union est Z ...

[Mikihisa]

Non enfait tu te méprends sur l'objet dont ont parle.

Enfait comm le l'ai expliquer, en réalité les élément de Z/nZ ne sont pas des nombre mais des ensemble. Il s'agit de "classe d'équivalence.

Par exemple prenons l'exemple de

En réalité = l'ensemble des entiers congru a 0 modulo 2 = l'ensemble des entier pair.
On peux effectivement faire l'analogie entre Z/2Z et l'ensemble {0,1} mais il faut être conscient de ce qui précède.

Je te met la façon dont j'ai fait la q1 dans l'après midi si tu veux.

[Waax22951]

Je comprends mieux, merci !
Cela veut dire que un nombre n'admet pas un inverse mais un ensemble d'inverses (si les conditions le permettent), c'est ça ? :hein:

Je pense avoir trouvé pour la réponse 1, et au final je crois avoir trouvé deux moyens de le démontrer, dont une qui n'utilise pas les congruences:

Première réponse:
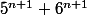
Supposons que F ne soit pas irréductible. Il existe donc un nombre premier p tel que p divise et p divise .
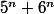
On en déduit que:
.
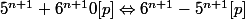
et
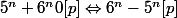
D'où
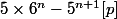
Donc .
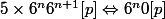
Donc p divise .
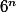
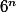
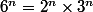
Puisque p est premier, p divise si et seulement si il apparaît dans sa décomposition en facteurs premiers. Or , donc p=2 ou p=3.

- Si p=2.
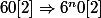
On a et .
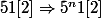
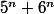
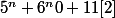
Or p divise , ce qui est absurde puisque . Donc p n'est pas égal à 2.

- Si p=3.
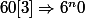
On a [3] et .
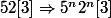
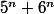
Or p divise , donc p divise (puisqu'ils sont congrus modulo 3). Puisque p est premier, p divise si et seulement si il apparaît dans sa décomposition en facteurs premiers. Or 3 n'apparaît pas dans la décomposition en facteur premiers de , donc le résultat est absurde. p est donc différent de 3.

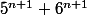
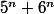
Il n'existe donc aucunes valeurs de p telles que p divise et p divise . Donc F est irréductible.

[CENTER]_________________________[/CENTER]

Seconde réponse:
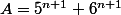
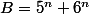
On pose et . On a donc .
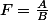
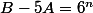
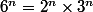
Supposons que F ne soit pas irréductible, il existe donc un nombre premier p tel que p divise A et p divise B. p divise donc toute combinaison linéaire de A et de B. Donc p divise . Or, p est premier, il apparaît donc dans la décomposition en facteurs premiers de . Donc p=2 ou p=3.
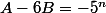
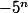
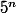
De même, p divise . Si p divise , alors il divise aussi . Il apparaît donc dans sa décomposition en facteurs premiers. Donc p=5.
On a donc p=5 et p=2 ou p=5 et p=3, ce qui est absurde, donc il n'existe pas de nombre premier divisant à la fois A et B, donc F est une fraction irréductible.

Voilà.. Dites moi si il y a une erreur de raisonnement, parce qu'apparemment, mon raisonnement en terme de divisibilité est loin d'être le meilleur ! :lol3:
Bonne après-midi !

PS: Je veux bien un corrigé si ça ne te dérange pas :lol3: .

PPS: Zygo: en effet, je n'avais pas pensé à ça, il faut vraiment que j'arrête de faire des maths le soir :lol3:

[Mikihisa]

Ma preuve ressemble beaucoup a ta première preuve, en fait il y avait une astuce qui rendait la tâche beaucoup plus facile.


Moi j'ai fait presque comme toi sauf que lui de passer 6^n de l'autre côté j'ai passer 5^n:

Donc on a p premier tel que
Donc :

Et
Donc
Donc finalement on a (en multipliant par -1 la première congruence puis par transitivité)
Donc p divise 5^n, or p est premier donc p=5.

Mais on a
Donc
Et
Donc

Ce qui est absurde car p divise

Ps : on ne trouve pas la même valeure de p et c'est tout a fait normal, ça ne veux pas dire que ton raisonnement est faux, en fait p n'existe pas et on raisonne par l'absurde pour le montrer, donc on trouve différente valeure pour p suivant le raisonnement, mais au final p n'existe pas.

[Waax22951]

D'accord, je comprends ! :lol3:
j'ai fait la moitié du travail pour la 2), je n'ai plus qu'à démontrer que si les deux produits sont premiers entre eux, alors la fraction est irréductible :)
Je vous préviens lorsque j'aurai terminé, histoire de voir si c'est vrai ! ;)

PS: mais cette petite erreur ne rend pas le raisonnement faux.. Si ? :hein:

[Mikihisa]

Pour la question 2) : Tu remarqueras que si F(n) n'est pas irréductible, on peux factoriser le numérateur et le dénominateur par un entier p premier. Et p divisera et p divisera en fait si p divise alors p divise car p est premier.
Maintenant je te laisse traduire ça en une condition sur les 4 entiers ( sur leurs pgcd respectifs par exemple )

Et c'est pas tout d'avoir la condition, il faut maintenant la démontrer


Non non ton raisonnement est bon, mais la conclusion n'es pas bonne car tu utilise une propriétés fausse pour conclure. Par contre pour p=2 aucun problème ^^, il fallais juste modifier un peu ta conclusion.

[Mikihisa]

J'ai modifier mon message car il ne me plaisait pas, si tu la lus avant éditing relis le :p

Voilà pl. faire compliquer quand on peux faire simple ^^ la ça me plait.


Aaaahh et si tu a l'impression que cette mini preuve par l'absurde suffit a prouver ce qu'on cherche, c'est parce qu'en fait on viens de montrer la partie "=>" de la CNS par contraposer ( (nonB=>nonA) <=> (A=>B)), on viens de montrer que "Si F(n) est irréductible alors on a P" ou P est la propriété ( que tu auras trouver déjà en lisant ce message j'espère ^^).
Le gros du travail maitenant c'est de montrer que P => F(n) irréductible.

Sur ce je te laisse a tes réflexion et j'vais faire mes maths a moi parce que j'ai du boulot aussi :p bon après-midi !

[Waax22951]

J'ai modifier mon message car il ne me plaisait pas, si tu la lus avant éditing relis le :p

Voilà pl. faire compliquer quand on peux faire simple ^^ la ça me plait.


Aaaahh et si tu a l'impression que cette mini preuve par l'absurde suffit a prouver ce qu'on cherche, c'est parce qu'en fait on viens de montrer la partie "=>" de la CNS par contraposer ( (nonB=>nonA) (A=>B)), on viens de montrer que "Si F(n) est irréductible alors on a P" ou P est la propriété ( que tu auras trouver déjà en lisant ce message j'espère ^^).
Le gros du travail maitenant c'est de montrer que P => F(n) irréductible.

Sur ce je te laisse a tes réflexion et j'vais faire mes maths a moi parce que j'ai du boulot aussi :p bon après-midi !

Non ne t'inquiète pas, je sais très bien qu'il faut aussi démontrer que l'implication est réciproque
En gros il me reste à démontrer que si les entiers sont premiers entre eux (enfin leur produit), alors la fraction est irréductible
(je suppose que l'on doit utiliser la fameuse propriété de .. ).
La propriété est bien " et sont premiers entre eux" ? :O

Pas de problèmes, je vais continuer aussi, bon aprèm' ! :lol3:

[Mikihisa]

Si p divise l.a alors p divise l ou p divise a.

La condition en fait est que l soit premier avec mu et beta et également que alpha soit premier avec mu et beta.
En d'autre terme :

Ps : j'ai dit une connerie, induit en erreur par l'aspect "absurde" de la preuve.

Si a et b sont congru modulo n et que n divise a, alors n divise b. En effet a et congru a 0modulo n et par transitivité b est aussi congru a 0 modulo n, donc en fait il n'y avait pas d'erreur dans ta preuve, mais tu t'es quand même pris la tête pour rien, vu que a partir du moment ou on avait 6^n+5^n congru a 2^n modulo 3, on avait que 3 ne divisait pas 6^n+5^n ce qui était en. Contradiction avec l'hypothèse, mae culpa.

[Mikihisa]

En fait non, je t'ai parler de Z/pZ uniquement pour la prospérité, la seule propriété que tu aura besoin ( enfin moi je l'ai utiliser sur mon corriger, que j'ai fait il y'a longtemps d'ailleurs :p) c'est la division des congruence, c'est a dire que :
Si a,b,c,d sont des entiers et p un nombre premier tels que c|a et d|b alors a/c est congru a b/d modulo p.

En effet cette propriété n'est vrai que si p est premier, elle est au programme de terminale ( spe maths), mais ce qui se cache derrière tout ça est un peu plus complexe et fait intervenir les classes d'équivalence de la congruence et donc les ensemble Z/nZ, c'était uniquement pour ta culture, tu pourras impressioner ta prof de maths et passer pour un nerd auprès de tes camarades de classe :D.

Exemple : 18~0[6], 9~3[6] avec 9|18 et 3|0 et pourtant 18/9 =2 n'est pas congru a 0/3=0 modulo 6. Donc il faut faire très attention avec cette propriété, elle n'est vrai QUE si p est premier.

[Waax22951]

En fait non, je t'ai parler de Z/pZ uniquement pour la prospérité, la seule propriété que tu aura besoin ( enfin moi je l'ai utiliser sur mon corriger, que j'ai fait il y'a longtemps d'ailleurs :p) c'est la division des congruence, c'est a dire que :
Si a,b,c,d sont des entiers et p un nombre premier tels que c|a et d|b alors a/c est congru a b/d modulo p.

En effet cette propriété n'est vrai que si p est premier, elle est au programme de terminale ( spe maths), mais ce qui se cache derrière tout ça est un peu plus complexe et fait intervenir les classes d'équivalence de la congruence et donc les ensemble Z/nZ, c'était uniquement pour ta culture, tu pourras impressioner ta prof de maths et passer pour un nerd auprès de tes camarades de classe .

Exemple : 18~0[6], 9~3[6] avec 9|18 et 3|0 et pourtant 18/9 =2 n'est pas congru a 0/3=0 modulo 6. Donc il faut faire très attention avec cette propriété, elle n'est vrai QUE si p est premier.

Je tourne en rond pour l'instant donc j'arrête pour ce soir (nouvelle résolution !). Je ne reprendrai pas l'exercice avant demain soir, voire mercredi midi, donc si je ne réponds pas, ce n'est pas que je n'y arrive pas, donc pas plus d'aide pour l'instant, j'aimerais voir si je suis capable d'y arriver seul ! (j'enverrai un message si je n'y arrive vraiment pas.. :lol3: ).
Je n'ai pas vu cette propriété dans mon cours d'arithmétique.. Il est sûrement au nouveau programme ou alors mon cours n'était pas complet !
Ne doit-on pas rajouter comme condition que les entiers sont non nuls et qu'ils sont différents de 1 ?
Car si on prend , , , et , on a:
.
Donc la fraction n'est pas réductible..
Je n'ai pas trouvé de démonstrations sur internet.. Où pourrais-je en trouver une s'il vous plaît ? (pour la division dans ).
Je passe déjà pour un nerd des maths auprès de mes amis, donc ça ne changera pas grand chose ! :ptdr:
Merci en tout cas pour toutes ces informations ! :lol3:

PS: J'ai juste une question complètement hors sujet. Si un corps est un ensemble dont chaque élément possède un inverse, alors qu'est-ce qu'un "idéal" ? J'en ai beaucoup entendu parlé, mais sa définition me semble incompréhensible..
Merci d'avance ! :lol3:

[Ingrid55]

En effet , ton cerveau parait déjà bien développé *.* ce qui est une bonne chose !

[Mikihisa]

Bah elle n'est peut être plus aborder ... En tous cas je suis sur d'avoir écrit ça dans mon cours en terminal S, mais bon c'était en 2009 lol
La j'ai pas vraiment la motivation mais j'essaierais une preuve demain. Quand a la division dans Z/pZ, a (sous entendu ici la classe de a) est inversible dans Z/nZ si pgcd(a;n)=1 (sous entendu ici le nombre a) donc si p est premier, pour tout a dans Z/pZ ( en faisait l'analogie abusive Z/pZ={0,...,p-1}) on a pgcd(a;p)=1 et donc tous élément a de Z/pZ est inversible.

En effet c'est probable qu'on suppose les entier différent de 1, en fait je n'ai plus l'énoncer exact c'était un bouquin qui s'appelait "oraux X-ENS" la plus part des exo sont de niveau MP* mais certains exo proposer ne requiert aucune notions particulières.

Je verrais tout ce demain bonne nuit.

Quant a l'idéal d'un anneau ... :lol5: encore faut il expliquer ce qu'est un anneau ^^
Je me ferais une joie d'éclairer ta lanterne, mais il faudrait pour bien faire les choses introduire d'inombrable notions, et si je ne me base que sur ce que tu es sence connaître du lycée, c'est a dire absolument rien en ce qui concerne l'algèbre j'ai pas fini.

Pour faire très concis, juste assez pour que tu ailles chercher des bouquins ^^ je te dirait :
"Définition : Un ensemble est une collections d'objet tous discernable par la pensée "
Lol la définition de l'ensemble...
L'idée des structure algébrique est de définir des "lois de composition" qui sont des applications qui a un couple d'objet (appeler éléments de l'ensemble) associe un objet de l'ensemble. Ce sont des des fonction de ExE --> E. (Exemple : l'addition, la multiplication,... Tous ce qui prend 2 objets pour en faire un seul quoi). Ensuite on définie des propriétés remarquable sur ces lois. Ainsi une structure algébrique est un ensemble muni d'une ou plusieurs lois, les propriété sur ces lois définissent alors des structure algébrique "remarquable" tels qu'on appel les Groupe, les Anneau, les Corps, ou encore les espaces vectoriels.
L'algèbre "général" est donc une approche très général des mathématiques ou l'ont ne raisonne plus sur des nombre mais sur des "objet" quelconques, appeler "elements" des ensembles.

Je m'arrête la, car je pense qu'il est préférable pour toi que tu abordes ces notions avec des bouquin plutôt que de te balancer des propriétés et des notions dans un pavé qui contiendras je n'en doute pas plein de coquilles, d'abus de langage, de manque de rigueur etc... :)

[Waax22951]

Bah elle n'est peut être plus aborder ... En tous cas je suis sur d'avoir écrit ça dans mon cours en terminal S, mais bon c'était en 2009 lol
La j'ai pas vraiment la motivation mais j'essaierais une preuve demain. Quand a la division dans Z/pZ, a (sous entendu ici la classe de a) est inversible dans Z/nZ si pgcd(a;n)=1 (sous entendu ici le nombre a) donc si p est premier, pour tout a dans Z/pZ ( en faisait l'analogie abusive Z/pZ={0,...,p-1}) on a pgcd(a;p)=1 et donc tous élément a de Z/pZ est inversible.

En effet c'est probable qu'on suppose les entier différent de 1, en fait je n'ai plus l'énoncer exact c'était un bouquin qui s'appelait "oraux X-ENS" la plus part des exo sont de niveau MP* mais certains exo proposer ne requiert aucune notions particulières.

Je verrais tout ce demain bonne nuit.

Quant a l'idéal d'un anneau ... :lol5: encore faut il expliquer ce qu'est un anneau ^^
Je me ferais une joie d'éclairer ta lanterne, mais il faudrait pour bien faire les choses introduire d'inombrable notions, et si je ne me base que sur ce que tu es sence connaître du lycée, c'est a dire absolument rien en ce qui concerne l'algèbre j'ai pas fini.

Pour faire très concis, juste assez pour que tu ailles chercher des bouquins ^^ je te dirait :
"Définition : Un ensemble est une collections d'objet tous discernable par la pensée "
Lol la définition de l'ensemble...
L'idée des structure algébrique est de définir des "lois de composition" qui sont des applications qui a un couple d'objet (appeler éléments de l'ensemble) associe un objet de l'ensemble. Ce sont des des fonction de ExE --> E. (Exemple : l'addition, la multiplication,... Tous ce qui prend 2 objets pour en faire un seul quoi). Ensuite on définie des propriétés remarquable sur ces lois. Ainsi une structure algébrique est un ensemble muni d'une ou plusieurs lois, les propriété sur ces lois définissent alors des structure algébrique "remarquable" tels qu'on appel les Groupe, les Anneau, les Corps, ou encore les espaces vectoriels.
L'algèbre "général" est donc une approche très général des mathématiques ou l'ont ne raisonne plus sur des nombre mais sur des "objet" quelconques, appeler "elements" des ensembles.

Je m'arrête la, car je pense qu'il est préférable pour toi que tu abordes ces notions avec des bouquin plutôt que de te balancer des propriétés et des notions dans un pavé qui contiendras je n'en doute pas plein de coquilles, d'abus de langage, de manque de rigueur etc...

D'accord.. Je regarderai ça plus tard alors ! :lol3:
(Je préfère me concentrer sur une seule chose à la fois..)
Une autre question me vient: existe-t-il des bons livres de vulgarisation en mathématiques ? Car les seuls que j'ai trouvé ne m'ont pas forcément convaincus.. :lol3:
Je retiens le nom du bouquin, il pourra peut-être me servir un jour ! :lol3:

[Mikihisa]

Pourquoi tu veux de la vulgarisation ^^ ? Les bouquin de deug / MPSI sont très bien, ils reprennent les choses en détails pour ce qui est de l'analyse, et pour l'algèbre de toute façon c'est tout nouveau donc.

Yavais un bouquin de MPSI pas mal, il abordait l'algèbre du tout début (théorie des ensemble, structure algébrique) pour finalement traiter des espace vectoriels (Algèbre De Jean Marie Monier je crois ). Le problème avec d'autre bouquin moins "scolaire" et plus "littéraire" c'est qu'ils partent souvent du principe que le lecteur est déjà a bac+2-3 en maths et lire ces bouquin peut vraiment devenir ennuyeux si tu n'as pas déjà quelque connaissance en la matière.

[Waax22951]

Pourquoi tu veux de la vulgarisation ^^ ? Les bouquin de deug / MPSI sont très bien, ils reprennent les choses en détails pour ce qui est de l'analyse, et pour l'algèbre de toute façon c'est tout nouveau donc.

Yavais un bouquin de MPSI pas mal, il abordait l'algèbre du tout début (théorie des ensemble, structure algébrique) pour finalement traiter des espace vectoriels (Algèbre De Jean Marie Monier je crois ). Le problème avec d'autre bouquin moins "scolaire" et plus "littéraire" c'est qu'ils partent souvent du principe que le lecteur est déjà a bac+2-3 en maths et lire ces bouquin peut vraiment devenir ennuyeux si tu n'as pas déjà quelque connaissance en la matière.

Je ne me considère pas forcément capable de lire des manuels scolaires de niveau prépa voire bac+3 ! :lol3:
Du coup je passe mon temps à lire des pages Wikipédia lorsque je cherche quelque chose, ce qui me frustre puisque certaines notions sont expliquées de manière brutes et n'offrent donc pas forcément (paradoxalement) la possibilité de les apprendre..!

[Mikihisa]

Les bouquin "scolaire" dont je te parles sont très bien fait, et particulièrement le bouquin d'algèbre, tu pourras le lire sans aucun problème je pense, a côté les articles Wikipedia sont bien plus rudes a lire, a mon avis. Après tout, ça reste des livre de 1ère année, et en 1ère année dans le sup (n math comme dans beaucoup de mentions) tu reprend tout a 0.
D'autant plus en algèbre que c'est des notion très basique qui pourtant ne sont pas abordé au lycée (une honte de faire des maths pendant ses 18 première année sans jamais entendre parler de théorie des nsemble ....)

[Waax22951]

Je regarderai alors ! :lol3:
Merci !
Juste une question: les entiers sont-ils tous positifs ou ils sont juste non nuls ? :hein:

[Waax22951]

Bon.. Je ne vais peut-être pas pouvoir continuer de chercher aujourd'hui, et le manque de temps m'obligeant à me dépêcher, je ne peux pas me permettre de tourner en rond.. :lol3:
Du coup je vais mettre mon début de réponse, et si je fais fausse route ou si j'ai faux, dites le moi s'il vous plaît ! :lol3:

(Je considère que n est non nul puisque si n est nul et que , , et , alors est irréductible alors que et sons tous les deux pairs)
Réponse:

On pose la propriété définie par:


Démontrons que pour tout entier naturel non nul n, est irréductible si et seulement si est vérifiée. Autrement dit, démontrons que pour tout entier naturel n, .

Tout d'abord, considérons le cas où est irréductible. On a alors:
.

D'après le théorème de Bézout, il existe deux entiers non nuls et tels que:
.


Par factorisation, on obtient:



.

Puisque , et .
Donc , , , , , , , sont des entiers naturels.

La réciproque du théorème de Bézout donc d'affirmer que:
(1): et sont premiers entre eux.
(2): et sont premiers entre eux.
(3): et sont premiers entre eux.
(4): et sont premiers entre eux.
Donc irréductible .


Considérons maintenant le fait que soit vraie et démontrons que est alors irréductible. Pour cela, supposons qu'il existe un n tel que n'est pas irréductible. Il existe donc un nombre premier p qui divise à la fois et .

On a alors:
et .
D'où et

Or , donc . On a aussi , donc .
On en déduit que

On en déduit aussi que:
.
Donc p divise . Il divise alors ou . S'il divise , il divise aussi . Or . Il divise alors à la fois et , ce qui est absurde puisqu'ils sont premiers entre eux.
Donc p divise . Donc .



Et à partir de là je ne vois pas comment arriver à un résultat absurde..