Recherche exercices arithmétique
Zygomatique ....
On suppose pas a et b réels. Le but est de trouver des solutions entière. Bon je vais quand même modifier l'énoncer pour te faire plaisir m'enfin bon le cas a=b ne nous intéresse pas vraiment.
Et le but c'est de faire de l'arithmétique, pas de passer par log(x)/x pour revenir aux entier.
Édit : Parce que x=y <=> ln(x)=ln(y) car ln est st monotone. Donc ln(a^b)=ln(b^a) <=> b.ln(a)=a.ln(b) et donc ln(a)/a=ln(b)/b
Tu étudie ma fonction ln(x)/x pour te rendre compte qu'elle change de sens de variation une seule fois en x=e, donc on a des solution réelles pour tout a dans ]0;e[ et de plus pour a dans ]0;e[ fixe le b qui correspond est unique ( car la fonction ne change qu'une seule fois de sens ).
Ensuite tu remarque que 2 est la seule valeure entière dans ]0;e[, et comme ln(2)/2 = 2ln(2)/2.2 = ln(4)/4, b=4 est la seule valeur qui convient pour a=2, et c'est aussi un entier donc tu as ton couple (2;4).
Mais c'est la preuve arithmétique qui est intéressante, pas la solution de facilité ^^
On suppose pas a et b réels. Le but est de trouver des solutions entière. Bon je vais quand même modifier l'énoncer pour te faire plaisir m'enfin bon le cas a=b ne nous intéresse pas vraiment.
Et le but c'est de faire de l'arithmétique, pas de passer par log(x)/x pour revenir aux entier.
Édit : Parce que x=y <=> ln(x)=ln(y) car ln est st monotone. Donc ln(a^b)=ln(b^a) <=> b.ln(a)=a.ln(b) et donc ln(a)/a=ln(b)/b
Tu étudie ma fonction ln(x)/x pour te rendre compte qu'elle change de sens de variation une seule fois en x=e, donc on a des solution réelles pour tout a dans ]0;e[ et de plus pour a dans ]0;e[ fixe le b qui correspond est unique ( car la fonction ne change qu'une seule fois de sens ).
Ensuite tu remarque que 2 est la seule valeure entière dans ]0;e[, et comme ln(2)/2 = 2ln(2)/2.2 = ln(4)/4, b=4 est la seule valeur qui convient pour a=2, et c'est aussi un entier donc tu as ton couple (2;4).
Mais c'est la preuve arithmétique qui est intéressante, pas la solution de facilité ^^
Ah oui en effet je n'avais pas remarqué !
(Je n'ai fait que lire le cours sur la continuité et le sens de variation d'une fonction donc ça ne me paraît pas encore évident de premier abord :lol3: )
Pour l'instant j'ai démontré que si a est impair si et seulement si b est impair et que a est pair si et seulement si b est pair, du coup je pense qu'en raisonnant par l'absurde, je peux en venir à une contradiction !
(Je suis pas sûr de pouvoir continuer aujourd'hui donc pas d'indices ni de solutions, merci ! :lol3: )
Bonne journée !
PS: qu'est-ce que l'oral de "l'X" ? ^^'
(Je n'ai fait que lire le cours sur la continuité et le sens de variation d'une fonction donc ça ne me paraît pas encore évident de premier abord :lol3: )
Pour l'instant j'ai démontré que si a est impair si et seulement si b est impair et que a est pair si et seulement si b est pair, du coup je pense qu'en raisonnant par l'absurde, je peux en venir à une contradiction !
(Je suis pas sûr de pouvoir continuer aujourd'hui donc pas d'indices ni de solutions, merci ! :lol3: )
Bonne journée !
PS: qu'est-ce que l'oral de "l'X" ? ^^'
Waax22951 a écrit:Je n'ai jamais vu cette notation, du coup j'ai toujours fait de cette façon, c'est plus un effort de rédaction qu'un réel changement :lol3:
Mais bon, je retiens quand même quand même, ça peut toujours servir..!
Je pense qu'il a simplement oublié de dire dans l'énoncer que a et b sont différents ^_^
Du coup je réfléchirai au problème posé demain
Juste une question, comment en es-tu venu à étudier la fonction? :we:
Bonne soirée !
ben le ppcm se définit par récurrence ...
p est multiple de 2, 3, 4, 5, 6, 7, 8 et 9
si p est multiple de 8 il est multiple de 2, 4 et 8
si p est multiple de 9 il est multiple de 3 et 9
si p est multiple de 8 et de 9 il est multiple de 2, 3, 4, 6, 8 et 9
reste 5 et 7 qui sont premiers ....
donc c'est plié en cinq sept ... :lol3:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
zygomatique a écrit:ben le ppcm se définit par récurrence ...
p est multiple de 2, 3, 4, 5, 6, 7, 8 et 9
si p est multiple de 8 il est multiple de 2, 4 et 8
si p est multiple de 9 il est multiple de 3 et 9
si p est multiple de 8 et de 9 il est multiple de 2, 3, 4, 6, 8 et 9
reste 5 et 7 qui sont premiers ....
donc c'est plié en cinq sept ... :lol3:
En réalité on peut dire que les propriétés du PPCM avec deux entiers sont les mêmes pour un nombre supérieur d'entiers, c'est ça ?
Cela ne fait qu'à peine deux semaines que je fais de l'arithmétique, je ne peux pas m'être posé toutes les questions. Après je pense que c'est en faisant des exercices qu'on se pose se genre de questions, donc si l'occasion ne s'était jamais présentée ^^'
Par exemple, même si je met énormément de temps à réussir l'exercice de Mikihisa, il m'a déjà appris beaucoup de choses :lol3:
Par exemple, même si je met énormément de temps à réussir l'exercice de Mikihisa, il m'a déjà appris beaucoup de choses :lol3:
bien sur c'est l'expérience donc la pratique qui conduit à se questionner ... qui font naitre les questions ....
mais l'important c''est que les questions naissent ... s'il n'y a jamais de question alors il n'y a pas d'apprentissage ....
mais l'important c''est que les questions naissent ... s'il n'y a jamais de question alors il n'y a pas d'apprentissage ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Le problème est que, pour ma part, je refuse de croire en une "intuition" lorsque je ne l'ai pas démontré, du coup je préfère demander lorsque je n'ai pas forcément le capacité ou juste lorsque je suis sur quelque chose d'autre :lol3:
(Par exemple je me suis posé une question en début d'année de première et je n'ai trouvé la solution que trois mois après, qui d'ailleurs était en contradiction avec mon idée de départ..).
Et ce que je n'aime pas avec l'arithmétique, ce n'est pas le fait que je ne me pose pas de questions, c'est que je ne me pose pas les bonnes.. Du coup je met beaucoup plus de temps..
(Par exemple je me suis posé une question en début d'année de première et je n'ai trouvé la solution que trois mois après, qui d'ailleurs était en contradiction avec mon idée de départ..).
Et ce que je n'aime pas avec l'arithmétique, ce n'est pas le fait que je ne me pose pas de questions, c'est que je ne me pose pas les bonnes.. Du coup je met beaucoup plus de temps..
Pour l'exo je te laisse quelques pistes en "spoiler" que tu pourras lire quand tu le souhaiteras !
Indice pour commencer :
Deux entier a et b sont premier entre eux si pgcd(a,b)=1. Ici tu remarque que a et b ne sont pas premier entre eux. Essai de le prouver ( deux nombre égaux on forcément la même décomposition en facteurs premier donc les même diviseurs premier ).
Indice pour commencer :
Deux entier a et b sont premier entre eux si pgcd(a,b)=1. Ici tu remarque que a et b ne sont pas premier entre eux. Essai de le prouver ( deux nombre égaux on forcément la même décomposition en facteurs premier donc les même diviseurs premier ).
J'ai maintenant un doute mais je suis quasiment sûr que a divise b.
Au pire j'expose ma piste la plus "poussée" et comme ça vous pourrez me dire si il y a une erreur ou si je fais fausse route :lol3:
Soit a et b deux entiers strictement positifs.
On pose:a^b=b^a)
Supposons d'abord que a=b, on a alors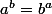 pour tout entiers naturels, donc le couple
pour tout entiers naturels, donc le couple ) avec
avec 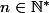 est solution
est solution
Supposons maintenant que a et b sont distincts et que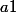 donc
donc 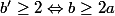 .
.
On remarque d'ailleurs que les premières valeur de a et de b sont=(2; 4)) , qui est un couple solution de (E).
, qui est un couple solution de (E).
Soit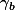 la propriété suivante:
la propriété suivante:
Pour tout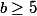 et pour tout entier a tel que
et pour tout entier a tel que 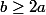 , l'équation
, l'équation :a^b=b^a) n'a aucune solutions triviales.
n'a aucune solutions triviales.
Pour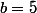 , on peut écrire:
, on peut écrire: :a^b=b^a \Leftrightarrow a^5=5^a) .
.
On sait que a est inférieur à 5, donc 5 ne divise pas a. 5 est un nombre premier donc a ne divise pas 5. Puisque a et 5 sont premier entre eux pour tout a, l'équation n'a pas de solutions. Donc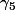 est vraie.
est vraie.
Supposons que est vraie pour un rang b et démontrons qu'elle est vraie au rang (b+1).
est vraie pour un rang b et démontrons qu'elle est vraie au rang (b+1).
Si a et b ne sont pas solutions, alors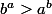 ou
ou 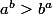 .
.
Et c'est là que ça bloque puisque je n'arrive pas à justifier que c'est vrai pour (b+1).
Le mieux que j'ai fait est:
^a>a^{b+1})
^a -ba^{b+1})
.. J'ai aussi conjecturé que si a et b ne sont pas solutions, alors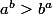 .. (On le vois nettement sur le graph de la fonction
.. (On le vois nettement sur le graph de la fonction 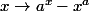 )..
)..
Du coup je me demande si je suis parti trop loin..
Au pire j'expose ma piste la plus "poussée" et comme ça vous pourrez me dire si il y a une erreur ou si je fais fausse route :lol3:
Soit a et b deux entiers strictement positifs.
On pose
Supposons d'abord que a=b, on a alors
Supposons maintenant que a et b sont distincts et que
On remarque d'ailleurs que les premières valeur de a et de b sont
Soit
Pour tout
Pour
On sait que a est inférieur à 5, donc 5 ne divise pas a. 5 est un nombre premier donc a ne divise pas 5. Puisque a et 5 sont premier entre eux pour tout a, l'équation n'a pas de solutions. Donc
Supposons que
Si a et b ne sont pas solutions, alors
Et c'est là que ça bloque puisque je n'arrive pas à justifier que c'est vrai pour (b+1).
Le mieux que j'ai fait est:
.. J'ai aussi conjecturé que si a et b ne sont pas solutions, alors
Du coup je me demande si je suis parti trop loin..
Tu dis que a divise b^a donc a divise b.
Ok b^a = b.b.b...b, mais alors b.b divise b^a et pourtant b.b ne divise pas b.
En fait oui a divise b, mais il faut pousser un peu plus pour le montrer.
Le reste semble pas mal du tout, je crois que la correction de l'exo était plus concis, mais reviens exactement au même ^^
Ok b^a = b.b.b...b, mais alors b.b divise b^a et pourtant b.b ne divise pas b.
En fait oui a divise b, mais il faut pousser un peu plus pour le montrer.
Le reste semble pas mal du tout, je crois que la correction de l'exo était plus concis, mais reviens exactement au même ^^
la récurrence ne peut pas marcher : ce n'est pas parce que a ne divise pas 5 que a ne divisera pas 5 + 1 = 6 ....
si d premier divise a alors d divise b
si d premier divise b alors d divise a
posons a = pd et b = qd avec (p, q) = 1
^{qd} = (qd)^{pd} p^{qd}(d^d)^q = q^{pd}(d^d)^p => p = q = 1 \ et \ a = b)
le seul autre cas qui reste est donc que b est une puissance de a
^a a^k = ka ...)
si d premier divise a alors d divise b
si d premier divise b alors d divise a
posons a = pd et b = qd avec (p, q) = 1
le seul autre cas qui reste est donc que b est une puissance de a
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
En effet Zygo c'est l'idée !
En fait on remarque que a et b ont les même diviseurs premiers.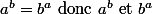 ont la même décomposition en facteurs premiers. Or les seuls diviseurs premiers de a^b sont ceux de a et les seuls diviseurs premier de b sont ceux de b. Donc a et b ont les même diviseurs premiers, donc pgcd(a;b)=\=1=d
ont la même décomposition en facteurs premiers. Or les seuls diviseurs premiers de a^b sont ceux de a et les seuls diviseurs premier de b sont ceux de b. Donc a et b ont les même diviseurs premiers, donc pgcd(a;b)=\=1=d
On a a=d.a' et b=d.b' donc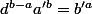 et cette fois ci pgcd(a',b')=1 ( si vous en êtes sceptique : comme a et b ont les même diviseurs premier, d est la produit de tout ces diviseurs)
et cette fois ci pgcd(a',b')=1 ( si vous en êtes sceptique : comme a et b ont les même diviseurs premier, d est la produit de tout ces diviseurs)
Ps: l'X c'est l'école polytechnique, quand tu passe le concours pour intégrer des grandes école comme l'X, les ENS etc... Tu passe une epreuve écrite et une épreuve orale qui dure 1h, on te propose un exercice qui est généralement un problème "ouvert" c'est a dire que tu peux le résoudre de plusieurs manière différente. C'est comme une "khole" que tu auras en prépa en fait.
En fait on remarque que a et b ont les même diviseurs premiers.
On a a=d.a' et b=d.b' donc
Ps: l'X c'est l'école polytechnique, quand tu passe le concours pour intégrer des grandes école comme l'X, les ENS etc... Tu passe une epreuve écrite et une épreuve orale qui dure 1h, on te propose un exercice qui est généralement un problème "ouvert" c'est a dire que tu peux le résoudre de plusieurs manière différente. C'est comme une "khole" que tu auras en prépa en fait.
zygomatique a écrit:la récurrence ne peut pas marcher : ce n'est pas parce que a ne divise pas 5 que a ne divisera pas 5 + 1 = 6 ....
Je ne dis pas que si a et b ne sont pas solution, alors ils sont premiers entre eux, je dis qu'il est nécessaire que a et b ne soient pas premiers entre eux, ce qui n'est pas le cas pour b=5.
Après je considère que si a^b est différent de b^a, alors l'un des deux est supérieur à l'autre, et je cherche à démontrer que c'est aussi le cas pour (b+1). J'ai conjecturé que a^b>b^a mais puisque je ne peux pas le démontrer, je ne peux pas m'en servir..
Mais après réflexion je pense qu'il y a une démonstration plus "arithmétique"..
En réalité j'ai marqué sur mon brouillon que b ne divise pas a car n est supérieur à a, j'ai juste oublié de l'écrire je pense
Après je ne sais pas si c'est suffisant de dire ça, mais je pense que si..
zygomatique a écrit:si d premier divise a alors d divise b
si d premier divise b alors d divise a
posons a = pd et b = qd avec (p, q) = 1
le seul autre cas qui reste est donc que b est une puissance de a
Comment arrive-t-on de
Je vais essayer pour
On a donc:
On remarque que si
On considère maintenant
Pour entier
Supposons maintenant que
On a donc:
D'où
Donc
Or
Une des conséquences immédiates est que l'équation
Donc l'ensemble des solutions de (E) avec a et b distincts sont l'ensemble des couples (a; k) avec
On remarque que:
On a démontré que (1) n'a pas de solutions pour
Donc
On a donc démontré que l'unique solution de (E) avec a et b distincts est (2; 4).
Waax22951 a écrit:Je ne dis pas que si a et b ne sont pas solution, alors ils sont premiers entre eux, je dis qu'il est nécessaire que a et b ne soient pas premiers entre eux, ce qui n'est pas le cas pour b=5.
Après je considère que si a^b est différent de b^a, alors l'un des deux est supérieur à l'autre, et je cherche à démontrer que c'est aussi le cas pour (b+1). J'ai conjecturé que a^b>b^a mais puisque je ne peux pas le démontrer, je ne peux pas m'en servir..
Mais après réflexion je pense qu'il y a une démonstration plus "arithmétique"..
En réalité j'ai marqué sur mon brouillon que b ne divise pas a car n est supérieur à a, j'ai juste oublié de l'écrire je pense
Après je ne sais pas si c'est suffisant de dire ça, mais je pense que si..
Comment arrive-t-on deà
?
Je vais essayer pour:
On a donc:donc
(1).
On remarque que si, alors
donc
.
On considère maintenant, la propriété suivante:
Pour entieret pour tout
, n3[/TEX].
est donc vraie.
Supposons maintenant queest vraie à un rang n et démontrons qu'elle est vraie au rang n+1.
On a donc:.
D'oùdonc
.
Donc
Orest vraie, donc pour tout
,
Une des conséquences immédiates est que l'équationn'a pas de solutions triviales pour
.
Donc l'ensemble des solutions de (E) avec a et b distincts sont l'ensemble des couples (a; k) avecet
.
On remarque que:.
On a démontré que (1) n'a pas de solutions pour.
Donc. On a donc
et
, donc l'unique solution de (1) est k=2.
On a donc démontré que l'unique solution de (E) avec a et b distincts est (2; 4).
quand deux nombres sont égaux c'est qu'ils ont le même facteur
effectivement quand j'écris a = pd et b = qd avec (p, q) = 1 alors d ne divise pas p et q en même temps
maintenant pour être plus rigoureux on peut rajouter la condition (p, d) = (q, d) = 1 ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
zygomatique a écrit:quand deux nombres sont égaux c'est qu'ils ont le même facteurà la même puissance ...
effectivement quand j'écris a = pd et b = qd avec (p, q) = 1 alors d ne divise pas p et q en même temps
maintenant pour être plus rigoureux on peut rajouter la condition (p, d) = (q, d) = 1 ....
Une question me vient à l'esprit: que signifie (p; q)=1 ? S'agit-il du PGCD ? :hein:
Je n'ai pas compris "quand deux nombres sont égaux c'est qu'ils ont le même facteur
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 104 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
