Question : suite
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
xie
- Membre Naturel
- Messages: 78
- Enregistré le: 15 Oct 2006, 21:56
-
 par xie » 24 Oct 2006, 20:40
par xie » 24 Oct 2006, 20:40
salut,
je bloque sur cette question :
soit
)
définie par :
 \;\;\;\; \forall n \in \mathbb{N}\\<br /> \end{array}<br /> \right.)
- je cherche à exprimer

en fonction de

et

.
pourriez-vous m'aider ?
merci :we:
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 24 Oct 2006, 21:58
par Quidam » 24 Oct 2006, 21:58
Que penserais-tu de définir la suite
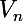
par

et d'étudier la suite
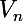
? C'est peut être plus facile !
-
xie
- Membre Naturel
- Messages: 78
- Enregistré le: 15 Oct 2006, 21:56
-
 par xie » 24 Oct 2006, 22:21
par xie » 24 Oct 2006, 22:21
re,
dsl pour le retard
oui j'ai déjà fait ça mais je vois pas comment ça peut m'aider :

quelle est la nature de
)
?
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 24 Oct 2006, 23:13
par Quidam » 24 Oct 2006, 23:13
xie a écrit:re,
dsl pour le retard
oui j'ai déjà fait ça mais je vois pas comment ça peut m'aider :

quelle est la nature de
)
?
Ben, si tu poses

Ta formule

te montre que

se situe au milieu entre

et

Ainsi,

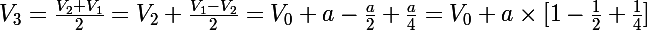
Tu dois facilement montrer par récurrence que :
^{n-1}}])
Entre crochets, tu as une somme partielle d'une série géométrique : tu sais donc la calculer !
-
xie
- Membre Naturel
- Messages: 78
- Enregistré le: 15 Oct 2006, 21:56
-
 par xie » 24 Oct 2006, 23:50
par xie » 24 Oct 2006, 23:50
re,
merci bcp Quidam :we:
oui j'ai réussi à démontrer cette formule avec une double reccurence , et pour l'expression voilà ce que je trouve :
^k}\right) = V_0 + \frac{1}{3}(V_1 - V_0) \left (2- \frac{(-1)^n}{2^{n-1}} \right))
i.e
 \left (2- \frac{(-1)^n}{2^{n-1}} \right) })
dites moi juste si c bon ou pas , vous m'avez déjà suffisemment aidé :++:
merci
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 25 Oct 2006, 04:07
par Zebulon » 25 Oct 2006, 04:07
Bonjour,
on est matinaux ce matin !
C'est aussi ce que je trouve (sans vérifier la récurrence cependant).
Bonne journée !
-
xie
- Membre Naturel
- Messages: 78
- Enregistré le: 15 Oct 2006, 21:56
-
 par xie » 25 Oct 2006, 04:19
par xie » 25 Oct 2006, 04:19
merci pour la comfirmation :we:
pour la reccurence j'en suis sure .
bonne journée

-
xie
- Membre Naturel
- Messages: 78
- Enregistré le: 15 Oct 2006, 21:56
-
 par xie » 25 Oct 2006, 19:56
par xie » 25 Oct 2006, 19:56
re,
je reviens sur ça , car il me parait de plus simple mais j'en suis pas sure .
on a

donc cette suite a pour équation caractéristique :

qui admet 2 solutions

ou

donc
^n + \beta (1)^n = \alpha \left(\frac{-1}{2}\right)^n + \beta)
ainsi :
 + \beta)
donc on obtient facilement :
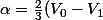)
et
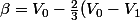)
soit :
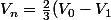 \left(\left(\frac{-1}{2}\right)^n + V_0 - 1 \right))
, d'ou on conclut l'expresion de

.
est-ce juste ? :hein:
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 25 Oct 2006, 21:37
par Quidam » 25 Oct 2006, 21:37
xie a écrit:est-ce juste ? :hein:
Je ne vérifie pas les calculs ! Je te fais confiance !
Bien sûr, il y a cette méthode générale ! Pourquoi pas ? Moi, j'ai trouvé que c'était tellement évident qu'il n'était pas utile de sortir cette méthode qui, elle, marche à tous les coups !
Bravo en tous cas de l'avoir appliquée !
-
xie
- Membre Naturel
- Messages: 78
- Enregistré le: 15 Oct 2006, 21:56
-
 par xie » 25 Oct 2006, 21:45
par xie » 25 Oct 2006, 21:45
merci bcp Quidam

en fait je savais pas que ça existe je viens de la trouver dans un bouquin .
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités
?