Question sur la limite d'une suite

[Skrilax]

Bonjour à tous,

Je viens de rencontrer une suite qui me pose quelques problèmes :



J'essaie de trouver la limite.

Voici ce que j'ai fait :

On a :

Donc,

Donc, ()

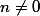
Donc,

Donc,

Bref, tout ça pour dire que la limite, si elle existe, est dans cet intervalle... lol

Y a-t-il moyen de faire mieux ?

[Clembou]

Bonjour à tous,

Je viens de rencontrer une suite qui me pose quelques problèmes :



J'essaie de trouver la limite.

Voici ce que j'ai fait :

On a :

Donc,

Donc, ()

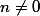
Donc,

Donc,

Bref, tout ça pour dire que la limite, si elle existe, est dans cet intervalle... lol

Y a-t-il moyen de faire mieux ?

Est-ce que tu as appris les équivalences ? Ici, on a affaire à une série donc l'étude de convergence est différente que celle d'une suite normale...

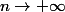
EDIT : Ah non, ce n'est pas vraiment une série. :triste: Quand , que peut-on dire de la valeur de pour tout

[Skrilax]

Est-ce que tu as appris les équivalences ? Ici, on a affaire à une série donc l'étude de convergence est différente que celle d'une suite normale...

Euh.. Quelle classe ?

[Clembou]

Euh.. Quelle classe ?

Je ne parle pas de classes d'équivalence mais plutôt de fonctions équivalentes.

Voir le EDIT dans mon premier message.

[Skrilax]

Non, je demandais en quelle classe on voyait ça ^^ :we:

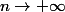
Quand , que peut-on dire de la valeur de pour tout

Ben on peut dire que ça tend vers 0, sauf que là, il y a une infinité de termes qui s'ajoutent, donc ça ne tend pas vers 0.

C'est faux ? :doh:

[Clembou]

Non, je demandais en quelle classe on voyait ça ^^ :we:



Ben on peut dire que ça tend vers 0, sauf que là, il y a une infinité de termes qui s'ajoutent, donc ça ne tend pas vers 0.

C'est faux ? :doh:

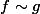
On le voit en première année de licence. On dit que (f est équivalent à g) en un point a si

Ah bon... Alors on m'aurait menti sur la valeur de :

:hein:

[Skrilax]

Ben justement, ici c'est pas



Mais plutôt



Avec M en réel qui tend vers 0.
Si tu additionne un nombre très très petit comme 10^-80 une infinité de fois, ça tend pas vers 0.

[Clembou]

Ben justement, ici c'est pas



Mais plutôt



Avec M en réel qui tend vers 0.
Si tu additionne un nombre très très petit comme 10^-80 une infinité de fois, ça tend pas vers 0.

Ok ! :++: Bon, on a que est une série. Est-ce que tu connais divers critères qui permettent d'étudier la convergence d'une série ?

[Skrilax]

Ok ! :++: Bon, on a que est une série. Est-ce que tu connais divers critères qui permettent d'étudier la convergence d'une série ?

Euh.. Ben écoute, je viens de finir mon année de première S lol...







:marteau: C'est quoi une série ? :marteau: =D

[Clembou]

Euh.. Ben écoute, je viens de finir mon année de première S lol...







C'est quoi une série ? :marteau: =D

Une série est une somme de termes d'une suite. On note .

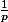
Essaie de prouver que est équivalent à d'après la définition que je t'ai donné.

[lapras]

Propriété : la limite d'une somme c'est la somme des limites.

Ce qu'a dit clambou est bon.

[Clembou]

Ce qu'a dit clambou est bon.

Heu :hein: C'est Clembou

Oui mais Lapras, je suis d'accord que la somme des limites est la limite de la somme. Mais ici, on a affaire à une somme infinie.

Il y a une propriété pour les séries qui dit que :

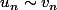
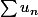
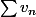
Si alors et ont la même nature (c'est-à-dire soient elles convergent, soient elles divergent).

[Skrilax]

Re, désolé pour le temps, je devais faire un truc avant tout.

Alors j'ai :



Donc ça tend vers 1, donc

C'est correct ?

[Clembou]

Re, désolé pour le temps, je devais faire un truc avant tout.

Alors j'ai :



Donc ça tend vers 1, donc

C'est correct ?

Ok ! Maintenant, il y a une propriété qui dit que : diverge (voir http://clement-boulonne.123.fr/cours/m203.pdf pour la démonstration). Que peut-on conclure sur la série ?

[Skrilax]

(Ah ok la pub dissimulée :we: ^^)

Non je rigole,merci beaucoup pour ton aide, je vais aller jeter un coup d'œil a tout hasard, mais je pense que trop de notions me sont encore inconnues.

Bon alors comme ça diverge...
Dommage :we:

PS = C'est à quelle page la démo ?

[Clembou]

(Ah ok la pub dissimulée :we: ^^)

Non je rigole,merci beaucoup pour ton aide, je vais aller jeter un coup d'œil a tout hasard, mais je pense que trop de notions me sont encore inconnues.

Bon alors comme ça diverge...
Dommage :we:

PS = C'est à quelle page la démo ?

La démonstration est page 13 :p

[emdro]

Je viens de rencontrer une suite qui me pose quelques problèmes :



J'essaie de trouver la limite.

Voici ce que j'ai fait :

On a :

Bonjour à tous,

A cause du ,je me demande si ce n'est pas au lieu de ...

Auquel cas, c'est bien différent...

[Clembou]

Bonjour à tous,

A cause du ,je me demande si ce n'est pas au lieu de ...

Auquel cas, c'est bien différent...

Ca reste quand même une série :zen:

[Clembou]

Bonjour à tous,

A cause du ,je me demande si ce n'est pas au lieu de ...

Auquel cas, c'est bien différent...

Je pense que c'est la même étude. Si , on est amené à l'étude d'une série...

[Skrilax]

o_O :doh: !

Quel boulet, j'ai fait un mix avec l'énoncé du dessous en recopiant !
Je suis sincèrement désolé, en fait c'est bien ce que t'avais dit emdro..

Mais ne t'inquiètes pas Clembou, tout ce que tu m'as dit n'auras pas servi à rien, parce que du coup, c'est la méthode de l'autre exo (en changeant juste les valeurs numériques) que je n'aurais, de toute façon, pas réussi au vu de la solution :we: