Question sur la limite d'une suite

[emdro]

Non, dans ce cas, la majoration de Skrilax (dans son premier post) est exacte, et la suite ne peut tendre vers l'infini.

Il s'agit alors d'une somme de Riemann... J'espère ne pas en avoir trop dit!

[Clembou]

Non, dans ce cas, la majoration de Skrilax (dans son premier post) est exacte, et la suite ne peut tendre vers l'infini.

Il s'agit alors d'une somme de Riemann... J'espère ne pas en avoir trop dit!

Ok ! J'ai vérifié ça sur MAPLE. Je pense, Skrilax, que la somme de cette série est une expression que tu n'as jamais vu (tu verras ça en TS).

[emdro]

Effectivement.
On peut quand même expliquer qu'en écrivant

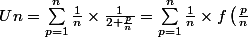avec ,
on reconnaît la somme des aires des petits rectangles de largeur 1/n situés sous la courbe de la fonction f entre 0 et 1.

Lorsque n tend vers l'infini, cette somme tend vers l'aire "sous la courbe" de f. Et c'est bien en TS que tu sauras l'exprimer.

[Joker62]

Entre Clembou qui lui fait bouffer des Séries et des équivalences, j'pense que le jeune homme n'est pas à ça près lol :D

J'ai trouvé ça capillotracté un peu ce post :)

[raito123]

Ce qu'a dit clambou est bon.

Non ce n'est pas toujours correcte !!

Tout à fait d'accord avec emdro : faut calculer l'intégral de f entre 0 et 1 !!!

[lapras]

Oui exactement. C'est la somme de 1 à n. Effectivement c'est l'intégrale de

[Skrilax]

Entre Clembou qui lui fait bouffer des Séries et des équivalences, j'pense que le jeune homme n'est pas à ça près lol

J'ai trouvé ça capillotracté un peu ce post

Ne t'inquiètes pas, je viens de télécharger un cours de calcul intégral pour pouvoir finir mon exo ^^

Je me suis farci le début tout ce matin, et je commence a avoir bien compris ^^

Donc, sujet à upper demain ^^