Merci Lycéen95 de ta réponse, cela va me permettre d'être + clair.

Alors:
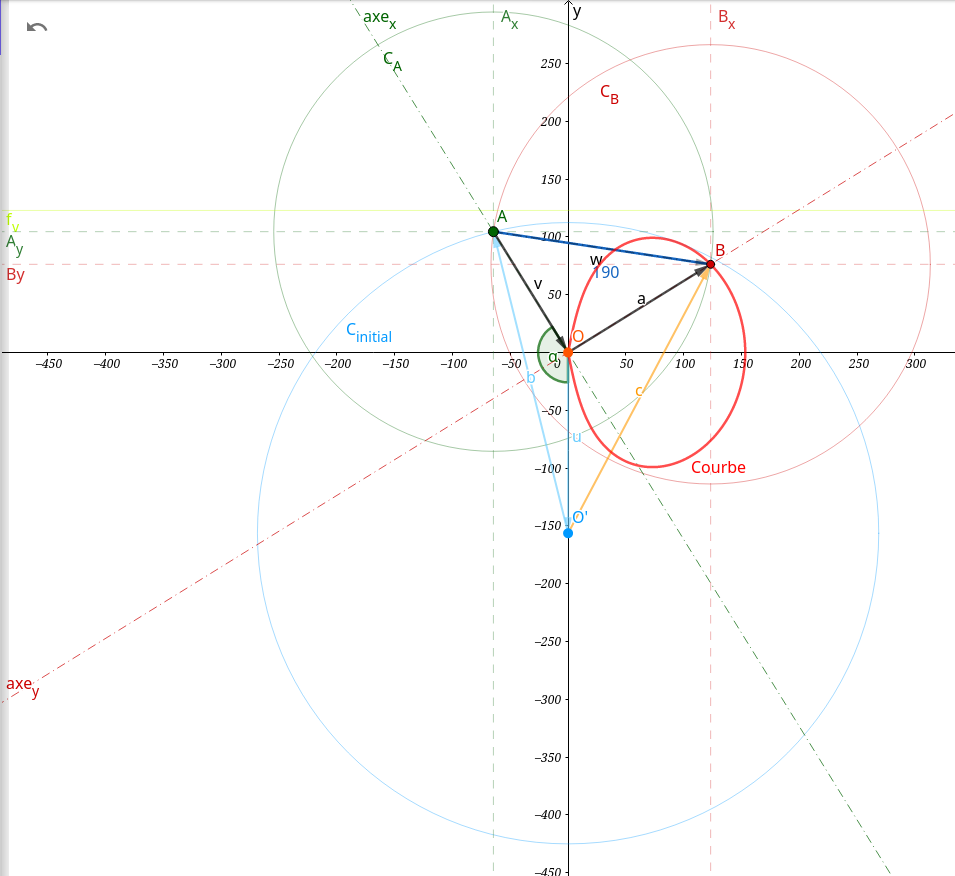
- Oui, dans un premier temps (ou plutôt dans une 1ere fonction(?) définie de x=-95 à x=95) le point A appartient bien au cercle C_initial de centre O'. (de rayon égal à la norme du vecteur b, *tant qu'on ne touche pas au point A...) Je cherche bien la courbe qui parcourt le "chemin" du point A puis, (à x=95) le chemin de B.
- (ou autrement dit) Je dis dans un premier temps, car je souhaite que le point A passe ensuite sur la courbe que décris le point B. Ce qui fait apparaître que les vecteurs b, c, v et a, ont des normes variables.
- La longueur AB (et "son" vecteur w) est bien fixe (100u.) Mais le point B ne "converge" vers le cercle C_initial qu'au point (95,95), uniquement. (en tout cas c'est ce que j'en attend

)
- Oui, le triangle AOB est toujours rectangle (en O).
Pour les "outils" :
- La trigo, c'était évident, vu le triangle, le repère orthonormé...
- J'ai pensé aux coordonnées polaires car je suppose (juste je suppose

) que ce sont aussi des vecteurs aux normes variables (v et a), qui tournent autour du centre O. (et vu qu'il ne faut qu'un angle, et une longueur pour définir un point avec des coordonnées polaires dans le plan....
- Une matrice de rotation ? non plus ? (j'en suis pas encore à ce niveau, mais en lisant un peu le sujet, j'ai aussi l'impression que ça pourrait être utile...(?) ) on pourrait considérer que le triangle OAB ne tourne pas (d'où mes axes en pointillés (axe_x et axe_y) colinéaires aux cotés OA et OB, et appliquer ensuite la rotation en O ? reste que la variation de OA n'est pas linéaire... (c'est bien le problème je crois !

)
Et oui

En connaissant l'angle AO'O, par Al-Kashi, j'ai la longueur OA (dans le triangle O'OA), je sais ensuite calculer la longueur OB par le théorème de Pythagore dans le triangle AOB. C'est pour ça qu'en voyant le dessin, "ça me parait simple"...

Tu dis:
"Il suffit juste de remplacer les coordonnées de A par XA et YA ... et d'écrire ces 2 nombres (XA,YA) en fonction de l'angle OO'A... et tu as résolu ton problème."
>> bin là, t'as beau être (peut-être) lycéen, tu m'as perdu


(avec tout mon respect

)
Je remplace mes valeurs par des coordonnées ?? non je suppose...
J'ai aussi mis des lettres pour chaque entité (segment, vecteurs, points...). T'as trouvé où R1 et R2 ??


(c'est moins clair pour moi du coup là


)
J'ai l'impression de devoir calculer 2 points en même temps...(?) ou calculer la position d'un segment en rotation autour de l'axe O....
Comme je dis, plus je regarde, plus je m'y perd...!!
(c'est comme avoir les clés de la voiture, sans savoir conduire, ni même en ouvrir sa porte....

)
*Je bug...
Si aucun Lycéen ne peux répondre à ça (vu que je post dans cette section) dans quelle rubrique devrais-je me trouver ? un appel aux modos (modérateurs) peut-être ?
Merci en tout cas de t'être penché sur le sujet. Sans me dire la réponse si tu penses l'avoir, as-tu trouvé la fonction (unique) qui trace la courbe passant par le chemin décrit par A, puis par B ??
Je répond à toute les questions