Probas, je nage !!
25 messages
- Page 1 sur 2 - 1, 2
probas, je nage !!
Bonjour,
Ca fait 15 ans que j'ai quitté l'école donc les probas sont loin derrière moi , mais j'ai repris des études et j'ai du mal. Voici l'exercice que j'ai à faire:
Claude range ses crayons de couleur et il en trouve 1 orange, 3 jaunes et 4 bleus. Il prend au hasard successivement 3 crayons dont il note les couleurs: O pour orange, J pour jaune et B pour bleu
Les réponses aux questions suivantes seront exprimées sous forme de fractions irréductibles.
1- quelle est la probabilité de l'évènement A: "les 3 crayons ont la même couleur" ?
2- Quelle est la probabilité de l'évènement B: "les 3 crayons sont pris parmi les crayons de couleur orange ou jaune" ?
3- Quelle est la probabilité de l'évènement C: " parmi les 3 crayons, un au moins est bleu" ?
4- Claude veut dessiner un drapeau bleu et jaune. Quelle est la probabilité qu'il puisse le faire sachant que le premier crayon est bleu ?
Je ne sais pas du tout comment aborder cet exercice, pouvez vous m'aider ?
Merci
Ca fait 15 ans que j'ai quitté l'école donc les probas sont loin derrière moi , mais j'ai repris des études et j'ai du mal. Voici l'exercice que j'ai à faire:
Claude range ses crayons de couleur et il en trouve 1 orange, 3 jaunes et 4 bleus. Il prend au hasard successivement 3 crayons dont il note les couleurs: O pour orange, J pour jaune et B pour bleu
Les réponses aux questions suivantes seront exprimées sous forme de fractions irréductibles.
1- quelle est la probabilité de l'évènement A: "les 3 crayons ont la même couleur" ?
2- Quelle est la probabilité de l'évènement B: "les 3 crayons sont pris parmi les crayons de couleur orange ou jaune" ?
3- Quelle est la probabilité de l'évènement C: " parmi les 3 crayons, un au moins est bleu" ?
4- Claude veut dessiner un drapeau bleu et jaune. Quelle est la probabilité qu'il puisse le faire sachant que le premier crayon est bleu ?
Je ne sais pas du tout comment aborder cet exercice, pouvez vous m'aider ?
Merci
Clembou a écrit:Il y a 8 crayons et il en prend 3 au hasard dans sa boite. Donc le nombre total de combinaisons est :
Ensuite pour chaque question, regarde les combinaisons possibles et pour avoir la proba, il faut diviser le nombre de combinaisons possibles avec le nombre de combinaisons total.
merci pour cette réponse mais je la comprends mal,
donc on a une combinaison de 3 sur 8 donc ma fraction en haute va être 8! mais pouquoi au dénominateur j'ai 3! 5! et pas seulement 3! ?
mon cours est super mal expliqué sur tout ce qui est combinaisons, arrangements...et j'ai quitté l'école y a 15 ans en sortant d'un bac littéraire, ça aide pas !! :marteau:
Bon, si je suis ce raisonnement que j'ai un peu mieux compris en regardant une video sur net prof
en introduction à la résolution de l'exercice, je cherhc e en fait le nombre de tirages possibles:
C \begin{pmatrix}3\\8\end{pmatrix} = 56 (zut j'arrive pas à l'écrire avec tex) C (3,8)
je dois ensuite déterminer pour 1) la probabilité de tirer 3 crayons de la meme couleur mais la j'arrive pas à le formuler de manière mathématique
en introduction à la résolution de l'exercice, je cherhc e en fait le nombre de tirages possibles:
C \begin{pmatrix}3\\8\end{pmatrix} = 56 (zut j'arrive pas à l'écrire avec tex) C (3,8)
je dois ensuite déterminer pour 1) la probabilité de tirer 3 crayons de la meme couleur mais la j'arrive pas à le formuler de manière mathématique
Oui, il y a un moyen mathématique. Disons que les combinaisons possibles sont :
 pour
pour 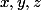 deux à deux différents. Combien y-a-t-il de possibilités pour que
deux à deux différents. Combien y-a-t-il de possibilités pour que 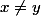 ,
,  ,
,  et que
et que  (c'est-à-dire que les valeurs possibles pour x,y,z sont 1, 2 et 3)...
(c'est-à-dire que les valeurs possibles pour x,y,z sont 1, 2 et 3)...
Pour les combinaisons avec les crayons bleues, c'est un peu plus dur...
Pour les combinaisons avec les crayons bleues, c'est un peu plus dur...
Il veut dire que lorsque tu comptes les tirages où les trois crayons sont sortis de la même couleur:
- il y a un seul tirage possible donnant trois crayons jaunes
- mais il y a *plus* d'un tirage possible donnant trois crayons bleus. En effet, il y a plusieurs façons de piocher trois crayons bleus parmi les *quatre* disponibles.
Donc au final, ta proba ne sera pas (1+1)/56, mais (1+X)/56, où X est le nombre de façons de tirer trois crayons bleus... que tu vas bien sûr trouver :-P
- il y a un seul tirage possible donnant trois crayons jaunes
- mais il y a *plus* d'un tirage possible donnant trois crayons bleus. En effet, il y a plusieurs façons de piocher trois crayons bleus parmi les *quatre* disponibles.
Donc au final, ta proba ne sera pas (1+1)/56, mais (1+X)/56, où X est le nombre de façons de tirer trois crayons bleus... que tu vas bien sûr trouver :-P
Bon, une première remarque au cas où (je sais plus de quelle question tu parlais^^) : tu as bien moins de 24 tirages possibles avec les 3 crayons de la même couleur.
Ensuite, pour compter le nombre de tirages avec les trois crayons bleus, la question que tu te poses en fait c'est:
"Combien y a t'il de façons de tirer un ensemble (non ordonné) de k éléments (ici, 3), parmi un ensemble plus grand (non ordonné) de n éléments (ici, 4)".
Dès que tu as une question comme ça, la réponse c'est .
.
++
Remarque :
Il est important de préciser que tes ensembles ne sont pas ordonnés ! Pour nous, tirer les crayons bleus dans l'ordre ou bien dans l'ordre
ou bien dans l'ordre  , c'est la même chose, et on ne le compte que comme *un* tirage. La seule chose qui nous intéresse c'est de savoir *quels* crayons bleus on a tiré. Dans cet exemple, donc, l'ensemble de crayons
, c'est la même chose, et on ne le compte que comme *un* tirage. La seule chose qui nous intéresse c'est de savoir *quels* crayons bleus on a tiré. Dans cet exemple, donc, l'ensemble de crayons  .
.
On pourrait aussi refaire tout le raisonnement précédent *en tenant compte de l'ordre* dans lequel on tire les crayons. Dans ce cas, il faut remplacer toutes les combinaisons par des arrangments
par des arrangments  , qui sont des nombres beaucoup plus grands (vu que ce qu'on appelait "un tirage" non ordonné peut correspondre à "plein de tirages" ordonnés). Mais ici, cette méthode ne sert à rien car elle rend les calculs plus embêtants pour, bien sûr, retrouver exactement la même probabilité au final !
, qui sont des nombres beaucoup plus grands (vu que ce qu'on appelait "un tirage" non ordonné peut correspondre à "plein de tirages" ordonnés). Mais ici, cette méthode ne sert à rien car elle rend les calculs plus embêtants pour, bien sûr, retrouver exactement la même probabilité au final !
Ensuite, pour compter le nombre de tirages avec les trois crayons bleus, la question que tu te poses en fait c'est:
"Combien y a t'il de façons de tirer un ensemble (non ordonné) de k éléments (ici, 3), parmi un ensemble plus grand (non ordonné) de n éléments (ici, 4)".
Dès que tu as une question comme ça, la réponse c'est
++
Remarque :
Il est important de préciser que tes ensembles ne sont pas ordonnés ! Pour nous, tirer les crayons bleus dans l'ordre
On pourrait aussi refaire tout le raisonnement précédent *en tenant compte de l'ordre* dans lequel on tire les crayons. Dans ce cas, il faut remplacer toutes les combinaisons
je pense que comme le tirage est " successif" et non simultané le card de l'univers est different , comme il y a 8 jetons , en tirant successivement 3 jetons il existe 8.7.6=336 possibilités de tirage.
p(A)=P(JJJ)+p(BBB)=3.2.1/336+4.3.2/336=5/56.
B est l'evenement obtenir des crayons Orange ou jaune
on calcul P(JJJ)=1/56 et p(OOO)=0
P( jaune ou orange ) =p(obtenir des crayons oranges)+p(obtenir des crayons jaunes)-P(jaune et orange )=0+1/56-1/56=0
p(A)=P(JJJ)+p(BBB)=3.2.1/336+4.3.2/336=5/56.
B est l'evenement obtenir des crayons Orange ou jaune
on calcul P(JJJ)=1/56 et p(OOO)=0
P( jaune ou orange ) =p(obtenir des crayons oranges)+p(obtenir des crayons jaunes)-P(jaune et orange )=0+1/56-1/56=0
25 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 86 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
