Primitive pour integrale
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
newton
- Membre Relatif
- Messages: 171
- Enregistré le: 02 Déc 2009, 13:47
-
 par newton » 27 Fév 2010, 14:06
par newton » 27 Fév 2010, 14:06
bonjour
je cherche une primitive pour une integrale dont je connais la reponse
mais je seche sur la primitive de f =t*racine(1+t²)
merci de me donner une piste

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 27 Fév 2010, 14:10
par Ericovitchi » 27 Fév 2010, 14:10
le changement de variable u=t²+1 va te ramener à trouver une primitive de
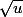
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 27 Fév 2010, 14:48
par benekire2 » 27 Fév 2010, 14:48
c'est franchement pas la peine, surtout que le changement de variable n'est pas nécessairement connue en Term.
Moi je dis qu'il faut réécrire :
en 1/2 * 2t*racine(1+t²)
on est sous la forme u' racine(u)
de là c'est déjà mieux
-
newton
- Membre Relatif
- Messages: 171
- Enregistré le: 02 Déc 2009, 13:47
-
 par newton » 27 Fév 2010, 14:51
par newton » 27 Fév 2010, 14:51
j ai pense a ca
2u racine(u)/3
mais apres
je precise que la reponse de l integralle S 1,2 =2/3racine2-1/3

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 27 Fév 2010, 15:08
par Ericovitchi » 27 Fév 2010, 15:08
la primitive de u' racine(u) c'est quoi ?
penses que racine de u c'est

-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 27 Fév 2010, 15:15
par benekire2 » 27 Fév 2010, 15:15
après on a pas dit que c'était la plus simple des primitive u'*racine(u)
mais ça a l'avantage de rester dans ce qu'on te demandera.
ici on a mis en évidence quelque chose de la forme f' * (g'of)
reste a trouver la primitive de g' qui est g :ptdr:
donc comme l'a dit erico x^(1/2) la primitive tu trouvera (2 x^(3/2))/3
t'as plus qu'a remplacé x par ton autre fonction : t²+1 et tu as ta primitive.
Sauf erreur.

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 27 Fév 2010, 15:25
par Ericovitchi » 27 Fév 2010, 15:25
(2 x^(3/2))/3 plutôt
-
newton
- Membre Relatif
- Messages: 171
- Enregistré le: 02 Déc 2009, 13:47
-
 par newton » 27 Fév 2010, 15:34
par newton » 27 Fév 2010, 15:34
je comprend pas
j ai vraiment du mal

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 27 Fév 2010, 15:48
par Ericovitchi » 27 Fév 2010, 15:48
Si tu dérives
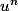
tu trouves quoi ? -->

Donc inversement une primitive de

c'est
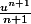
(dérives là tu va bien retomber sur

-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 27 Fév 2010, 15:52
par benekire2 » 27 Fév 2010, 15:52
Ericovitchi a écrit:(2 x^(3/2))/3 plutôt
oui plutôt excuse.
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 27 Fév 2010, 15:55
par benekire2 » 27 Fév 2010, 15:55
newton a écrit:je comprend pas
j ai vraiment du mal
tu m'as pas dit la dernière fois que t'avais jamais fais ni primitivation ni calcul intégral?
-
newton
- Membre Relatif
- Messages: 171
- Enregistré le: 02 Déc 2009, 13:47
-
 par newton » 27 Fév 2010, 20:46
par newton » 27 Fév 2010, 20:46
on vient de commencer en soutien vendredi
-
newton
- Membre Relatif
- Messages: 171
- Enregistré le: 02 Déc 2009, 13:47
-
 par newton » 27 Fév 2010, 21:13
par newton » 27 Fév 2010, 21:13
je propose d ailleurs
F=t²/2*2(1+t²)racine(1+t²)/3
ce qui colle au resultat de l integral donné par le prof sur 1,0 = 2/3racine2-1/3
enfin pour moi
la prochaine j essaierai avec les balises tex
-
newton
- Membre Relatif
- Messages: 171
- Enregistré le: 02 Déc 2009, 13:47
-
 par newton » 28 Fév 2010, 06:42
par newton » 28 Fév 2010, 06:42
j espere que la premiere est correct pour vous
voila une autre
(t+2)(t+3)}{t^2}dt)
j ai tenté de developper pour avoir

mais apres ??? et je suis pas sur du tout de l idée
le resultat doit faire 11ln2+21/2

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 28 Fév 2010, 10:37
par Sa Majesté » 28 Fév 2010, 10:37

et tu intègres chacun des termes
-
newton
- Membre Relatif
- Messages: 171
- Enregistré le: 02 Déc 2009, 13:47
-
 par newton » 28 Fév 2010, 13:52
par newton » 28 Fév 2010, 13:52
oui j ai trouve la derniere
mais pour l autre avant je suis pas sure

sqrt{1+t^2}}{3})

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 28 Fév 2010, 13:58
par Ericovitchi » 28 Fév 2010, 13:58
une primitive de

c'est ça dont tu veux la confirmation ?
C'est
^{3/2})
donc tu as un t² en trop semble t-il
-
newton
- Membre Relatif
- Messages: 171
- Enregistré le: 02 Déc 2009, 13:47
-
 par newton » 28 Fév 2010, 14:26
par newton » 28 Fév 2010, 14:26
pour

j avais fait

et pour t ben t²/2
deplus comme je dois trouver

et que ma calcu me donne comme primitive
 sqrt{1+t^2}}{3})
je cherche mais ne trouve pas

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 28 Fév 2010, 14:34
par Ericovitchi » 28 Fév 2010, 14:34
oui et bien ça va.
On trouve bien pareil car
\sqrt{1+t^2}}{3}=\frac{(1+t^2)^{3/2}}{3})
je te signale.
-
newton
- Membre Relatif
- Messages: 171
- Enregistré le: 02 Déc 2009, 13:47
-
 par newton » 28 Fév 2010, 19:44
par newton » 28 Fév 2010, 19:44
oui d accord mais ques que je fais de mon t en t²/2 avant
)
je sais que c est la ou je bloque
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités
