Nombres premiers

par **eva** » 11 Nov 2005, 22:09

Bonsoir à tous !

1. Factoriser 2431 puis rechercher les nombres entiers naturels

et

s'écrivant

.

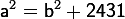
2. a) Soit

=

où les termes

sont des nombres premiers et les

des entiers naturels non nuls. Démontrer que si touts les nombres

sont pairs, alors

est un carré parfait (c'est-à-dire le carré d'un entier). Démontrer la réciproque.

b) Déterminer le plus petit entier naturel par lequel il faut multiplier 240 pour obtenir un carré parfait.

c) Déterminer les nombres

de cinq chiffres (notation décimale) dont le chiffre des unités est un 9, qui sont multiples de 147 et qui sont des carrés parfaits.

3. Soit

l'entier qui s'écrit en système décimal avec n chiffres 1. Montrer que si

est premier alors n est premier. La réciproque est-elle vraie?

Merci pour toute aide car à part la factorisation en facteurs premiers... je suis un peu perdue.

par **Galt** » 11 Nov 2005, 22:47

Une fois que 2431 est factorisé, l'équation s'écrit

et une brave identité remarquable va faire le travail à ta place.
2 a) Si

, alors

Réciproquement, le carré d'un produit de facteurs

va donner ?
b) 240=16*3*5. Que faire^pour rendre les exposants pairs ?
c) Le nombre 11111...111 peut s'écrire 1 + 10 +100 + 1000+...+1000000000, somme d'une suite géométrique, on peut l'écrire

, et si n est un produit pq, on peut écrire

et factoriser le numérateur

par **eva** » 12 Nov 2005, 18:22

1. (a + b)(a - b)

= 11

= 143

= 187

= 221

2. b) 240 =

, le plus petit entier naturel par lequel il faut multiplier 240 pour obtenir un carré parfait est donc 3

= 15 pour avoir

c) faut-il partir de N =

= 10000a + 1000b + 100c + 10d + 9 ?
je n'arive pas à raisonner sur cette question...

par **becirj** » 12 Nov 2005, 18:42

. Pour avoir un carré parfait, il faut donc au moins multiplier par 3 (question précédente). Le nombre cherché est don un multiple de 147 x 3 =441.
IL faut le multiplier par un carré parfait pour avoir un nombre de 5 chiffres.
Comme le nombre cherché se termine par 9, il faut multiplier 441 par un carré parfait dont le chiffre des unités est 9 . Les nombres sont le carré se termine par 9 sont les nombres dont le chiffre des unités est 3 ou 7.
On trouve un premier nombre avec

441 x 49 = 21609
Deuxième possibilité :

441 x 169=74529 .
Avec 17 , on obtient un nombre de 6 chiffres donc il n'y a que 2 possibilités.

par **eva** » 13 Nov 2005, 17:49

oki merci! est-ce que pour la 3. on peut démontrer la contraposée? c'est-à-dire montrer qui si n n'est pas premier alors \frac{10^n -1} {9} n'est pas premier...
pour voir si la réciproque est vraie ou non suffit-il de trouver un contre exemple?

par **becirj** » 13 Nov 2005, 19:14

Bonsoir

La réponse est oui aux deux questions :
Pour démontrer que

premier implique n premier, on peut démontrer la contraposée : n non premier implique

non premier.
Pour démontrer qu'une propriété n'est pas vérifiée, un contre-exemple suffit.

par **eva** » 13 Nov 2005, 20:09

le problème, c'est que je ne trouve pas de contre exemple... faut-il essayer de démontrer que n premier n'implique pas forcément

premier ? qqn a -t-il une idée pour cela?

par **becirj** » 13 Nov 2005, 20:22

Il faut un contre exemple avec n premier et

non premier. Il suffit de prendre n= 3 premier tandis que 111=3 x 37

par **eva** » 13 Nov 2005, 20:42

ah oui! lol merci! j'avoue avoir fait 5, 7, 13 et les autres mais j'ai même pas réussi à prendre simplement 3 :marteau:

par **eva** » 14 Nov 2005, 20:58

j'ai une petite question pour la 3. le nombre qui s'écrit avec n chiffres 1, ne va-til pas s'écrire

?? par exemple pour le nombre s'écrivant avec 5 chiffres 1 va s'écrire

est-ce que la somme est bien égale à

?

par **becirj** » 14 Nov 2005, 21:12

L'écriture de la somme est bien exacte mais c'est une somme de n termes consécutifs d'une suite géométrique de raison 10 et de premier terme 1 donc cette somme est bien égale à

par **eva** » 14 Nov 2005, 21:21

ah oui le n représente le nombre de termes...

par **eva** » 17 Nov 2005, 18:06

Bonsoir!

becirj a écrit: Les nombres dont le carré se termine par 9 sont les nombres dont le chiffre des unités est 3 ou 7.

Je me demandais s'il était nécessaire de démontrer ceci? :hein: si oui, comment peut-on faire?
Merci

par **becirj** » 17 Nov 2005, 18:13

Il suffit de faire un petit tableau avec sur une première ligne le chiffre des unités de nde 0 à 9 et sur la seconde ligne le chiffre des unités correspondant de

pour voir que seuls 3 et 7 conviennent.

par **eva** » 17 Nov 2005, 20:01

merci! :zen:

par **Florentin** » 06 Nov 2014, 18:52

Bonjour, alors moi aussi j'ai un petit ( quoi que...) soucis. J'espere que vous allez pouvoir m'eclaircir au plus tot...
La question est la suivante : Quel est le plus petit entier par lequel il faut multiplier 879 pour obtenir un carré parfait ?
J'aurais voulu avoir le resultat, oui , mais surtout la facon de faire ( sinon aucun interet...)
Alors ?? :mur:
MERCI D'AVANCE

par **nodjim** » 06 Nov 2014, 19:04

Décompose 879 en un produit de facteurs premiers, ensuite tu pourras facilement trouver le multiple carré parfait.

par **Florentin** » 06 Nov 2014, 19:55

nodjim a écrit:Décompose 879 en un produit de facteurs premiers, ensuite tu pourras facilement trouver le multiple carré parfait.

Comme decomposition, je propose 3x293 =879 ( 293 et 3 etant des nombres premiers ) et ensuite !?

par **Ben314** » 06 Nov 2014, 20:12

http://www.maths-forum.com/a-l-aide-159831.php

Nombres premiers

nombres premiers

Qui est en ligne