Nombres Complexes Ts!
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Vuittoni
- Membre Naturel
- Messages: 98
- Enregistré le: 31 Mai 2008, 16:54
-
 par Vuittoni » 03 Oct 2008, 20:45
par Vuittoni » 03 Oct 2008, 20:45
Bonsoir à tous, j'ai un petit problème au niveau de mon dm sur les nombres complexes.
Voici l'énoncé :
Soit le nombre complexe a=;)(2-;)3)-i;)(2+;)3)
1. Calculer a², puis déterminer son module er un argument.
Je pose donc a²=;)(2-;)3)-i;)(2+;)3)²
Et je développe sa comme une identité remarquable, (a+b)²=a²+2ab+b².. et je tombe sur un nombre très bizarre..
Merci de me dire mon erreur.
-
Monsieur23
- Habitué(e)
- Messages: 3966
- Enregistré le: 01 Oct 2006, 17:24
-
 par Monsieur23 » 03 Oct 2008, 20:58
par Monsieur23 » 03 Oct 2008, 20:58
Ben dis nous donc quel est ce nombre bizarre...
« Je ne suis pas un numéro, je suis un homme libre ! »
-
Vuittoni
- Membre Naturel
- Messages: 98
- Enregistré le: 31 Mai 2008, 16:54
-
 par Vuittoni » 03 Oct 2008, 21:02
par Vuittoni » 03 Oct 2008, 21:02
Monsieur23 a écrit:Ben dis nous donc quel est ce nombre bizarre...
donc a^2=(;)(2-;)3)-i;)(2+;)3)^)2
=-6-2rac2-6irac2-rac3
Je ne sais pas du tout si mon développement est juste.
En développant (;)(2-;)3))^2 je trouve -7.. je doute que ce soit juste mon raisonnement.
Merci
-
Monsieur23
- Habitué(e)
- Messages: 3966
- Enregistré le: 01 Oct 2006, 17:24
-
 par Monsieur23 » 03 Oct 2008, 21:07
par Monsieur23 » 03 Oct 2008, 21:07
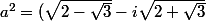^2 \\<br />a^2 = \sqrt{2-\sqrt3} ^2 - \sqrt{2+\sqrt3} ^2 - 2i \sqrt{2+\sqrt3} \sqrt{2-\sqrt3})
En développant (;)(2-;)3))^2 je trouve -7
Comment trouves-tu ça ?
Le carré de la racine d'un nombre positif, c'est ce nombre, tout simplement.
« Je ne suis pas un numéro, je suis un homme libre ! »
-
Vuittoni
- Membre Naturel
- Messages: 98
- Enregistré le: 31 Mai 2008, 16:54
-
 par Vuittoni » 03 Oct 2008, 21:18
par Vuittoni » 03 Oct 2008, 21:18
Monsieur23 a écrit: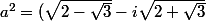^2 \\<br />a^2 = \sqrt{2-\sqrt3} ^2 - \sqrt{2+\sqrt3} ^2 - 2i \sqrt{2+\sqrt3} \sqrt{2-\sqrt3})
Comment trouves-tu ça ?
Le carré de la racine d'un nombre positif, c'est ce nombre, tout simplement.
Je trouve 7-rac7-8i.. en faisant autrement, jmen sort pas avec les racines,
(rac(2-rac3))^2 je trouve rac(4-3) donc rac1 donc 1...
-
Vuittoni
- Membre Naturel
- Messages: 98
- Enregistré le: 31 Mai 2008, 16:54
-
 par Vuittoni » 03 Oct 2008, 21:24
par Vuittoni » 03 Oct 2008, 21:24
Vuittoni a écrit:Je trouve 7-rac7-8i.. en faisant autrement, jmen sort pas avec les racines,
(rac(2-rac3))^2 je trouve rac(4-3) donc rac1 donc 1...
J'ai maintenant un atre résultat, 10-4i, cela me semble plus cohérent.
-
Monsieur23
- Habitué(e)
- Messages: 3966
- Enregistré le: 01 Oct 2006, 17:24
-
 par Monsieur23 » 04 Oct 2008, 12:21
par Monsieur23 » 04 Oct 2008, 12:21

, c'est tout !
« Je ne suis pas un numéro, je suis un homme libre ! »
-
Vuittoni
- Membre Naturel
- Messages: 98
- Enregistré le: 31 Mai 2008, 16:54
-
 par Vuittoni » 04 Oct 2008, 17:50
par Vuittoni » 04 Oct 2008, 17:50
Monsieur23 a écrit:
, c'est tout !
J'ai trouvé 12i et je crois bien que c'est sa, car on en cherchant le module je trouve rac144, ce qui fait 12 et dans les questions suivantes il est au dénominateur.
-
Monsieur23
- Habitué(e)
- Messages: 3966
- Enregistré le: 01 Oct 2006, 17:24
-
 par Monsieur23 » 04 Oct 2008, 18:20
par Monsieur23 » 04 Oct 2008, 18:20
Je trouve a² = - 2 Rac(3) - 2i
« Je ne suis pas un numéro, je suis un homme libre ! »
-
Vuittoni
- Membre Naturel
- Messages: 98
- Enregistré le: 31 Mai 2008, 16:54
-
 par Vuittoni » 04 Oct 2008, 18:28
par Vuittoni » 04 Oct 2008, 18:28
Monsieur23 a écrit:Je trouve a² = - 2 Rac(3) - 2i
Oula, en faite, la ou je m'en sort pas c'est avec 2*(rac(2-rac3)*irac(2+rac3)..
je ne sais pas comment faire...
Merci
-
Monsieur23
- Habitué(e)
- Messages: 3966
- Enregistré le: 01 Oct 2006, 17:24
-
 par Monsieur23 » 04 Oct 2008, 18:29
par Monsieur23 » 04 Oct 2008, 18:29
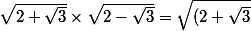(2-\sqrt3)})
Avec ça tu devrais t'en sortir !
« Je ne suis pas un numéro, je suis un homme libre ! »
-
Vuittoni
- Membre Naturel
- Messages: 98
- Enregistré le: 31 Mai 2008, 16:54
-
 par Vuittoni » 04 Oct 2008, 18:35
par Vuittoni » 04 Oct 2008, 18:35
Monsieur23 a écrit: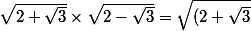(2-\sqrt3)})
Avec ça tu devrais t'en sortir !
Sa fait rac1.?
-
Monsieur23
- Habitué(e)
- Messages: 3966
- Enregistré le: 01 Oct 2006, 17:24
-
 par Monsieur23 » 04 Oct 2008, 18:46
par Monsieur23 » 04 Oct 2008, 18:46
Ouép.
Donc 1 en fait.
« Je ne suis pas un numéro, je suis un homme libre ! »
-
Vuittoni
- Membre Naturel
- Messages: 98
- Enregistré le: 31 Mai 2008, 16:54
-
 par Vuittoni » 04 Oct 2008, 18:49
par Vuittoni » 04 Oct 2008, 18:49
Monsieur23 a écrit:Ouép.
Donc 1 en fait.
donc c'est -2i*1= 2i
-
Monsieur23
- Habitué(e)
- Messages: 3966
- Enregistré le: 01 Oct 2006, 17:24
-
 par Monsieur23 » 04 Oct 2008, 19:01
par Monsieur23 » 04 Oct 2008, 19:01
Euh
-2i * 1 = -2i
« Je ne suis pas un numéro, je suis un homme libre ! »
-
Vuittoni
- Membre Naturel
- Messages: 98
- Enregistré le: 31 Mai 2008, 16:54
-
 par Vuittoni » 04 Oct 2008, 19:09
par Vuittoni » 04 Oct 2008, 19:09
Monsieur23 a écrit:Euh
-2i * 1 = -2i
Je ne vois pas du tout comment vous trouver ce résultat: a² = - 2 Rac(3) - 2i
, comment obtenez vous -2rac3???
Moi a la fin j'ai 2-rac3-2i+2+rac3..
=4-2i.
-
Monsieur23
- Habitué(e)
- Messages: 3966
- Enregistré le: 01 Oct 2006, 17:24
-
 par Monsieur23 » 04 Oct 2008, 19:37
par Monsieur23 » 04 Oct 2008, 19:37
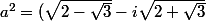^2 \\a^2 = \sqrt{2-\sqrt3} ^2 - \sqrt{2+\sqrt3} ^2 - 2i \sqrt{2+\sqrt3} \sqrt{2-\sqrt3})
Donc il reste bien 2 - Rac(3) - ( 2 + Rac(3) ) comme partie réelle !
« Je ne suis pas un numéro, je suis un homme libre ! »
-
Vuittoni
- Membre Naturel
- Messages: 98
- Enregistré le: 31 Mai 2008, 16:54
-
 par Vuittoni » 04 Oct 2008, 19:44
par Vuittoni » 04 Oct 2008, 19:44
Monsieur23 a écrit: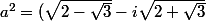^2 \\<br /> a^2 = \sqrt{2-\sqrt3} ^2 - \sqrt{2+\sqrt3} ^2 - 2i \sqrt{2+\sqrt3} \sqrt{2-\sqrt3})
Donc il reste bien 2 - Rac(3) - ( 2 + Rac(3) ) comme partie réelle !
Dèje votre formule me semble fausse, (a-b)^2=a^2-2ab+b^2, donc une erreur de signe je crois bien, dans ce que vous trouver, et les racines, normalement s'annulent...
-
Monsieur23
- Habitué(e)
- Messages: 3966
- Enregistré le: 01 Oct 2006, 17:24
-
 par Monsieur23 » 04 Oct 2008, 19:45
par Monsieur23 » 04 Oct 2008, 19:45
N'oublies pas qu'il y a un "i" qui traine.
i² = -1
« Je ne suis pas un numéro, je suis un homme libre ! »
-
Vuittoni
- Membre Naturel
- Messages: 98
- Enregistré le: 31 Mai 2008, 16:54
-
 par Vuittoni » 04 Oct 2008, 19:50
par Vuittoni » 04 Oct 2008, 19:50
Monsieur23 a écrit:N'oublies pas qu'il y a un "i" qui traine.
i² = -1
Oui, exacte, mais même comment pouvez vous trouvez 2rac3 alors qu'il n'y a pas de multilication la?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 70 invités
