DM TS nombres complexes
17 messages
- Page 1 sur 1
DM TS nombres complexes
Bonjour à tous j'ai un dm à rendre dont voici l'énoncé des 2 premiers exercices :
Exercice 1:
Soit le polynôme P(z)= z^3 - 2z² + z - 2, où z est un nombre complexe
a) Calculer P(i) et P(2).
b) Déterminer les réels a et b tels que, pour tout complexe z, P(z)= (z-2)(az²+b)
Résoudre alors P(z) = 0 dans C.
c) Pour tout complexe z =/ -1, résoudre l'équation ((z-1)/(z+1))^3 -2((z-1)/(z+1))² + (z-1)/(z+1) - 2=0.
Exercice 2: Une équation particulière... Résoudre l'équation z²-4z/ -5 =0 dans C.
J'ai trouvé comme réponse à la question a) que P(i)=i^3 +i et que P(2)=0, mais à la question b je ne vois pas de quelle manière procéder pour trouver les réels a et b qu'on me demande de déterminer et pour l'exercice 2, je ne sais pas comment résoudre une équation du second degré comportant le nbr complexe z et son conjugué, il me faudrait savoir quelle est la partie réelle et imaginaire de Z. Je vous remercie d'avance pour votre aide.
Exercice 1:
Soit le polynôme P(z)= z^3 - 2z² + z - 2, où z est un nombre complexe
a) Calculer P(i) et P(2).
b) Déterminer les réels a et b tels que, pour tout complexe z, P(z)= (z-2)(az²+b)
Résoudre alors P(z) = 0 dans C.
c) Pour tout complexe z =/ -1, résoudre l'équation ((z-1)/(z+1))^3 -2((z-1)/(z+1))² + (z-1)/(z+1) - 2=0.
Exercice 2: Une équation particulière... Résoudre l'équation z²-4z/ -5 =0 dans C.
J'ai trouvé comme réponse à la question a) que P(i)=i^3 +i et que P(2)=0, mais à la question b je ne vois pas de quelle manière procéder pour trouver les réels a et b qu'on me demande de déterminer et pour l'exercice 2, je ne sais pas comment résoudre une équation du second degré comportant le nbr complexe z et son conjugué, il me faudrait savoir quelle est la partie réelle et imaginaire de Z. Je vous remercie d'avance pour votre aide.
Re: DM TS nombres complexes
Salut,
a) que fait i^3 ?
b) développe P(z)=(z-2)(az²+b) puis identifie les coefficients de ce polynôme avec P(z)= z^3 - 2z² + z - 2
a) que fait i^3 ?
b) développe P(z)=(z-2)(az²+b) puis identifie les coefficients de ce polynôme avec P(z)= z^3 - 2z² + z - 2
Re: DM TS nombres complexes
Pas du tout avec la marche à suivre demandée, et donc juste pour info :
Il fut un temps où on aurait fait ceci :
P(z)= z^3 - 2z² + z - 2
P(z)= z²(z - 2) + z - 2
P(z)= (z - 2).(z²+1)
P(z)= (z - 2).(z² - i²)
P(z)= (z - 2).(z - i).(z + i)

Il fut un temps où on aurait fait ceci :
P(z)= z^3 - 2z² + z - 2
P(z)= z²(z - 2) + z - 2
P(z)= (z - 2).(z²+1)
P(z)= (z - 2).(z² - i²)
P(z)= (z - 2).(z - i).(z + i)
Re: DM TS nombres complexes
merci à tous pour vos réponses, effectivement je n'avais pas fais attention que je pouvais simplifier i^3 ce qui rend plus clair, par contre je ne vois pas en quoi faire de cette facon va me permettre de déterminer des réels ni que P(z)= (z-2)(az²+b). Et, en remplaçant z²-4z/ par x+iy et x-iy, je trouve :
(x+iy)²-4(x-iy)-5=x² + 2xiy -y² -4x +4iy -5; mais ça ne me simplifie pas du tout l'écriture au contraire.
(x+iy)²-4(x-iy)-5=x² + 2xiy -y² -4x +4iy -5; mais ça ne me simplifie pas du tout l'écriture au contraire.
Re: DM TS nombres complexes
DragonArgentetOr a écrit: par contre je ne vois pas en quoi faire de cette facon va me permettre de déterminer des réels ni que P(z)= (z-2)(az²+b)
Tu développes tu as
Or
Donc la tu peux identifier les coefficients de ce polynôme et tu obtiens a et b.
Modifié en dernier par infernaleur le 30 Déc 2017, 12:35, modifié 1 fois.
Re: DM TS nombres complexes
DragonArgentetOr a écrit: Et, en remplaçant z²-4z/ par x+iy et x-iy, je trouve :
(x+iy)²-4(x-iy)-5=x² + 2xiy -y² -4x +4iy -5; mais ça ne me simplifie pas du tout l'écriture au contraire.
Il faut déjà essayer de simplifier (développer etc ...) avant de dire que sa ne simplifie pas l'écriture.
[edit : je n'avais pas tout lu et vu que tu avais développé pardon]
Modifié en dernier par infernaleur le 30 Déc 2017, 18:40, modifié 1 fois.
Re: DM TS nombres complexes
DragonArgentetOr a écrit:merci à tous pour vos réponses, effectivement je n'avais pas fais attention que je pouvais simplifier i^3 ce qui rend plus clair, par contre je ne vois pas en quoi faire de cette facon va me permettre de déterminer des réels ni que P(z)= (z-2)(az²+b). Et, en remplaçant z²-4z/ par x+iy et x-iy, je trouve :
(x+iy)²-4(x-iy)-5=x² + 2xiy -y² -4x +4iy -5; mais ça ne me simplifie pas du tout l'écriture au contraire.
En partant de x² + 2xiy -y² -4x +4iy -5=0
tu résous le système
Re: DM TS nombres complexes
ok j'ai compris ce que vous vouliez faire avec ça, donc j'ai réussi, et après pour résoudre P(z)=0, j'ai fait z-2=0 ou z²+1=0 et j'ai trouvé 3 solutions, en revanche pr l'exo 2, pour résoudre un système je dois prendre quoi comme expressions : x²+2xiy-y² et -4x+4iy-5?
Re: DM TS nombres complexes
Salut
Pisigma t'a tout dit
x² + 2xiy -y² -4x +4iy -5=0
(x² - y² - 4x - 5) + i.(2xy + 4y) = 0
Un nombre complexe est nul si et seulement si sa partie réelle est nulle ET sa partie imaginaire est nulle.
La partie réelle du nombre complexe (x² - y² - 4x - 5) + i.(2xy + 4y) est (x² - y² - 4x - 5)
La partie imaginaire du nombre complexe (x² - y² - 4x - 5) + i.(2xy + 4y) est (2xy + 4y)
Et donc ...

Pisigma t'a tout dit
x² + 2xiy -y² -4x +4iy -5=0
(x² - y² - 4x - 5) + i.(2xy + 4y) = 0
Un nombre complexe est nul si et seulement si sa partie réelle est nulle ET sa partie imaginaire est nulle.
La partie réelle du nombre complexe (x² - y² - 4x - 5) + i.(2xy + 4y) est (x² - y² - 4x - 5)
La partie imaginaire du nombre complexe (x² - y² - 4x - 5) + i.(2xy + 4y) est (2xy + 4y)
Et donc ...
Re: DM TS nombres complexes
Pour limiter les calculs on peut aussi conjuguer l'expression de départ et soustraire membre à membre
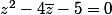
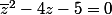
d'où(z+\bar{z}+4)=0)
donc (z est réel et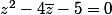 ) ou (Re(z)=-2 et
) ou (Re(z)=-2 et 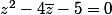 )
)
d'où
donc (z est réel et
Re: DM TS nombres complexes
ok, j'ai compris, je pensais que c'était qu'avec les produits qu'on pouvait résoudre un système comme ça, du coup j'ai réussi à résoudre le système, merci de votre aide, par contre pour la dernière question, vu qu'il y a un cube, je ne peux pas utilise delta?
Re: DM TS nombres complexes
Où vois-tu un problème à cause d'un cube ?
Si c'est pour répondre à la question 1c ... alors tu n'as pas compris l'essentiel.
En ayant démontré que P(z)= z^3 - 2z² + z - 2, pouvait s'écrire P(z) = (z - 2).(z - i).(z + i)
Résoudre P(z) = 0 est immédiat, on a comme solution :
z1 = 2 ; z2 = i et z3 = -i
*****
Il s'agit maintenant de résoudre : ((z-1)/(z+1))^3 -2((z-1)/(z+1))² + (z-1)/(z+1) - 2=0.
Qui est identique à z^3 - 2z² + z - 2 = 0 dans lequel on aurait remplacé z par (z-1)/(z+1)
On a donc, par comparaison avec le début de l'exercice :
a) (z-1)/(z+1) = 2 d'où on doit déduire z = ...
b) (z-1)/(z+1) = i d'où on doit déduire z = ...
c) (z-1)/(z+1) = -i d'où on doit déduire z = ...
Pas de problème avec un cube.

Si c'est pour répondre à la question 1c ... alors tu n'as pas compris l'essentiel.
En ayant démontré que P(z)= z^3 - 2z² + z - 2, pouvait s'écrire P(z) = (z - 2).(z - i).(z + i)
Résoudre P(z) = 0 est immédiat, on a comme solution :
z1 = 2 ; z2 = i et z3 = -i
*****
Il s'agit maintenant de résoudre : ((z-1)/(z+1))^3 -2((z-1)/(z+1))² + (z-1)/(z+1) - 2=0.
Qui est identique à z^3 - 2z² + z - 2 = 0 dans lequel on aurait remplacé z par (z-1)/(z+1)
On a donc, par comparaison avec le début de l'exercice :
a) (z-1)/(z+1) = 2 d'où on doit déduire z = ...
b) (z-1)/(z+1) = i d'où on doit déduire z = ...
c) (z-1)/(z+1) = -i d'où on doit déduire z = ...
Pas de problème avec un cube.
Re: DM TS nombres complexes
ah d'accord, en fait pour la question b) j'avais fais un truc bien plus compliqué que ça, et j'avais trouvé un z2 et un z3 avec des racines. De plus, à cause de la forme fractionnaire, je n'avais pas saisi que c'était une transformation du z de l'équation de départ, là je comprends pourquoi le cube n'a pas besoin d'être résolu.
Re: DM TS nombres complexes
enfin, dans mon dernier exercice, on me demande de déterminer la limite d'une fonction ha en +00,définie pour tout nombre réel a, sur R par ha(x)= (ax + 1/2)/e^x. J'aimerais savoir si je m'y suis pris de la bonne façon:
lim ax=+00
x>+00
a>+00
lim e^x=+00
x>+00
a>+00
lim ax +1/2=+00
x>+00
a>+00
On a une Fi: "00/00"
et après je ne sais pas si je dois factoriser pour trouver la limite?
lim ax=+00
x>+00
a>+00
lim e^x=+00
x>+00
a>+00
lim ax +1/2=+00
x>+00
a>+00
On a une Fi: "00/00"
et après je ne sais pas si je dois factoriser pour trouver la limite?
Re: DM TS nombres complexes
Salut.
Méthode 1)
Retenir qu'une exponentielle "gagne" toujours sur une puissance ... et donc la limite est 0 (c'est ce qu'on fait en Secondaire)
Méthode 2)
On est dans un cas où la règle de Lhospital est d'application et donc on trouve de suite que la limite est 0 (si on connait la règle évidemment)
Méthode 3)
On utilise un développement de e^x
e^x = 1 + x + x²/2! + ...+ x^n/(n!) + ...
e^x < 1 + x + x²/2! (pour x > 0)
|ha(x)| = |ax+1/2|/e^x
|ha(x)| = |ax+1/2|/e^x
0 <= |ax+1/2|/(1 + x + x²/2! ) (pour x > 0)
0 <= lim(x-->+oo) |ha(x)| < lim(x-->+oo) |ax + 1/2|/(1 + x + x²/2!)
0 <= lim(x-->+oo) |ha(x)| < 0
lim(x-->+oo) |ha(x)| = 0
Il reste un peu de boulot (pas beaucoup) pour montrer la monotonie de g(x) = (ax + 1/2), pour conclure.
Et plein d'autres méthodes ...

Méthode 1)
Retenir qu'une exponentielle "gagne" toujours sur une puissance ... et donc la limite est 0 (c'est ce qu'on fait en Secondaire)
Méthode 2)
On est dans un cas où la règle de Lhospital est d'application et donc on trouve de suite que la limite est 0 (si on connait la règle évidemment)
Méthode 3)
On utilise un développement de e^x
e^x = 1 + x + x²/2! + ...+ x^n/(n!) + ...
e^x < 1 + x + x²/2! (pour x > 0)
|ha(x)| = |ax+1/2|/e^x
|ha(x)| = |ax+1/2|/e^x
0 <= |ax+1/2|/(1 + x + x²/2! ) (pour x > 0)
0 <= lim(x-->+oo) |ha(x)| < lim(x-->+oo) |ax + 1/2|/(1 + x + x²/2!)
0 <= lim(x-->+oo) |ha(x)| < 0
lim(x-->+oo) |ha(x)| = 0
Il reste un peu de boulot (pas beaucoup) pour montrer la monotonie de g(x) = (ax + 1/2), pour conclure.
Et plein d'autres méthodes ...
17 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
