Nombre complexe

[xD55]

Bonjour, pouvez-vous m'aider à résoudre l'exercice suivant:
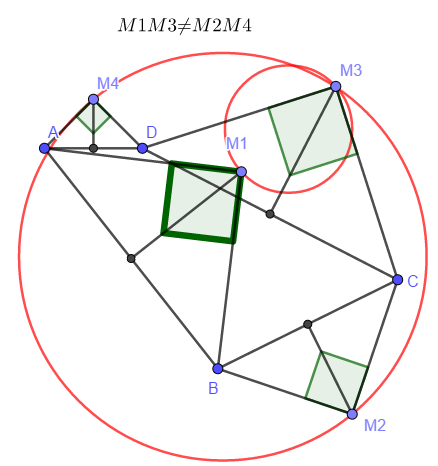
soit ABCD un quadrilatere convexe . Extérieurement au quadrilatere on construit le point M1(resp M2,M3,M4) tel que AM1B ( resp B2C , CM3D, DM4A) soit un triangle isocele de sommet principal M1(resp M2,M3,M4) .Soit a,b,c et d le affixes respectives de A,B,C et D . z1,z2,z3 et les affixes respectives de M1,M2,M3 et M4

1)a) montrer que b-z1/a-z1= i . en deduire z1 en fonction de a et b
b) ecrire z2,z3 et z4 en fonction de a , b ,c et d
2) montrer que les vecteurs M1M3 et M2M4 sont orthogonaux et ont la meme norme .
Pouvez-vous m'aider et merci bcp

[pascal16]

"soit un triangle isocele de sommet principal M1"

c'est pas "soit un triangle isocele et rectangle de sommet principal M1"

[xD55]

pascal16 c'est ce que j ai trouve dans l enonce
cette exercice est difficile ou non ???

[GaBuZoMeu]

Tu as oublié de choses en recopiant l'énoncé. Par exemple tu as clairement oublié . Tu as sans doute aussi oublié "un triangle isocèle rectangle".

[xD55]

oui c est vrai
dsl c est ma faute . maintenant comment continuer l exercice s il vous plait GaBuZoMeu

[GaBuZoMeu]

On a dû t'apprendre le lien entre multiplication par et rotation d'un quart de tour dans le sens direct, n'est-ce pas ?

[vladi]

2) montrer que les vecteurs M1M3 et M2M4 sont orthogonaux et ont la meme norme .

bonjour

il semble qu'il manque quelque chose à l'énoncé en plus que les triangles sont isocèles rectangles
il n'ont pas forcément la même norme là dans la figure

[vladi]

Extérieurement au quadrilatere on construit le point M1(resp M2,M3,M4) tel que...

dans la figure du post précédent , M1 est situé à l'extérieur du quadrilatère

pour vérifier l'égalité des normes des deux vecteurs l'énoncé correct ne serait-il pas?

tous les points situés strictement à l'intérieur des triangles isocèles rectangles doivent êtres situés à l'exterieur du quadrilatère?

[vladi]

Bonjour

Quand l'auteur de ce sujet me confirmera que dans l'énoncé il fallait aussi dire ce que j'ai dit précédemment

alors je pourrais faire l'exo* sinon comment expliquer la figure que j'ai placé dans mon précédent post?

une fois que ce sera confirmé alors je fais remarquer que :

En ce qui concerne le quadrilatère

l'ensemble des quadrilatères convexes du plan est



À partir de là 1)2)3)4) est obligatoirement vérifié

1)il existe un point du plan tel que d'une part est un triangle non plat

et d'autre part est situé à l'intérieur du triangle

et d'autre part avec

et

2)il existe un point du plan tel que d'une part est un triangle non plat

et d'autre part est situé à l'intérieur du triangle

et d'autre part avec

et

3)il existe un point du plan tel que d'une part est un triangle non plat

et d'autre part est situé à l'intérieur du triangle

et d'autre part avec

et

4)il existe un point du plan tel que d'une part est un triangle non plat

et d'autre part est situé à l'intérieur du triangle

et d'autre part avec

et

*sans confirmation je fais l'exo mais je suis obligé de modifier l'énoncé

[vladi]

...En attendant la réponse à ma question posée à l'auteur de ce sujet et concernant le problème de l'inégalité des normes des deux vecteurs dans certains cas si on suit à la lettre l'énoncé tel qu'il est donné et même si les triangles sont isocèles rectangles et même si les sont situés à l'extérieur du quadrilatère convexe(voir la figure plus haut)
je proposais de rectifier l'énoncé en stipulant qu'il fallait que tous les points situés strictement à l'intérieur de ces triangles soient tous situés à l'extérieur du quadrilatère
__________________
...bref en attendant

je propose ici d'écrire autrement l'ensemble de tous les quadrilatères convexes ABCD

cette manière de l'écrire est plus pratique que la précédente



remplacer les trois petits points par





c'est vrai que l'écriture est plus longue que la précédente mais pour se donner tout quadrilatère convexe

c'est plus pratique car il suffit de se donner tous (réels)

[GaBuZoMeu]

Tu en fais peut-être un peu beaucoup, là, vladi ?

[vladi]

Tu en fais peut-être un peu beaucoup, là, vladi ?

je m'excuse
cet exo est trop joli(je le continue chez moi mais je ne poste rien )

[xD55]

vladi j ai rectifie le sujet il manque juste rectangle et z4 pour les affixes si tout .
et merci beaucoup

[vladi]

vladi j ai rectifie le sujet il manque juste rectangle et z4 pour les affixes si tout .
et merci beaucoup

mais alors comment expliquez vous la figure plus haut ?

les M1,M2,M3,M4 sont bien à l'extérieur du quadrilatère, les triangles sont isocèles rectangles

et vous me dites (dans votre énoncé) que les deux vecteurs et ont même norme

sur la figure on voit bien que non

tandis que si on corrige votre énoncé en stipulant que tous les points strictement à l'intérieur des triangles isocèles rectangles sont à l'exterieur du quadrilatère là ça marche

[xD55]

donc il y a une faute d énoncé .
en tt cas je vous dis encore merci bcp .

[GaBuZoMeu]

Non, il n'y a pas faute d'énoncé, vladi fait un peu de zèle.
Il y a plutôt un implicite couramment admis : construire extérieurement sur le côté d'un polygone convexe, c'est construire dans le demi-plan délimité par la droite support du côté et qui ne contient pas les autres sommets du polygone.
Il y a par contre une imprécision de l'énoncé qui est peut-être levée par un dessin l'accompagnant : les sommets A, B, C, D du quadrilatère sont décrits dans le sens des aiguilles d'une montre (contrairement au dessin de vladi). On s'en aperçoit en lisant la première question de l'énoncé.

Revenons à cette question : xD55, as-tu compris mon indication concernant le lien entre rotation d'un quart de tour dans le sens direct et multiplication par ?

[xD55]

Revenons à cette question : xD55, as-tu compris mon indication concernant le lien entre rotation d'un quart de tour dans le sens direct et multiplication par ?

sincèrement j ai pas compris mr

[GaBuZoMeu]

Alors il faudrait sans doute que tu revoies ton cours sur l'utilisation des nombres complexes en géométrie.
Vu l'exercice, tu as sûrement eu un cours sur ce sujet, non ?

[GaBuZoMeu]

Rappel de cours : le point Q d'affixe q s'obtient à partir du point P d'affixe p par une rotation d'un quart de tour (dans le sens direct) de centre O d'affixe o si et seulement si
q-o = i*(p-o).

[vladi]

Non, il n'y a pas faute d'énoncé, vladi fait un peu de zèle.
Il y a plutôt un implicite couramment admis : construire extérieurement sur le côté d'un polygone convexe, c'est construire dans le demi-plan délimité par la droite support du côté et qui ne contient pas les autres sommets du polygone.

ah oui je vois (je n'avais pas vu la réponse) : l'implicite de la construction du point à l'extérieur implique qu'on sous-entend que c'est aussi valable pour le triangle

(à retenir)

merci GaBuZoMeu