Maths spécialité

[erloup]

Bonjour,
Notre proffesseur nous a donné un exercice et je suis coincé sur les question 3 et 4. Voila le sujet:
Equation (E) : 10x-27k = m où x et k des entiers relatifs et m est un paramètre entier non nul.
1) Justifier en énoncant un théorème, qu'il existe un couple (u, v) tel que 10u-27v = 1, trouver un tel couple.
Ma réponse: PGCD(10, 27) = 1 d'après le théorème de Bézout il existe un tel couple. Et j'ai trouvé (-8, 3)

2) En déduire une solution particulière (x0, k0) de l'équation en fonction de m
Ma réponse: si le paramètre m vaut 0, alors une solution particulière est (-8, 3)

3) Montrer que (x, k) est soltuion de (E) si et seulement si 10(x-x0)-27(k-k0) = 0
4) En déduire que les solutions de (E) sont exactements les couples d'entiers relatifs (x, k) tels qu'on a q entiers relatifs avec:
x = -8m+27q
{
y = -3m+10q

Voila je suis bloqué sur la question 3 et 4. Merci de votre aide.

[GaBuZoMeu]

Reprends depuis le début. Tu commences avec une erreur de signe : ne fait pas 1.
Ensuite, tu réponds n'importe quoi à la question 2. N'importe quoi, parce que ta réponse est fausse (même en corrigeant l'erreur de signe) : fait 1 et pas 0. Et n'importe quoi parce qu'on demande une solution particulière fonction de , qui marche pour tout !
J'ai l'impression que tu fais un mélange entre l'indice 0 dans et le fait de faire .
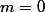Voyons, ce n'est pas compliqué : tu sais que

et tu veux un couple en fonction de tel que
.

[erloup]

Oui je me suis trompé j'avais bien le couple (-8, -3). Donc pour la question 2 et 3 on doit faire ça ou pas :
2) On sait que 10*(-8)-27*(-3) = 1
Donc 10*(-8m)-27*(-3m) = m
On prend x(0) = -8m et k(0) = -3m
Alors 10x(0)-27k(0) = m
Donc une solution particulaire est (-8m, -3m)
3) On sait que 10x-27k = m et que 10x(0)-27k(0) = m
Donc on les soustrait :
10x-10x(0)-27k+27k(0) = m-m
↔ 10(x-x(0))-27(k-k(0)) = 0

[GaBuZoMeu]

2) Ce n'est pas une solution particulaire (pas grand chose à voir avec la physique des particules) mais une solution particulière.
3) La rédaction ne va pas.
"On sait que 10x-27k = m "
Non, on ne sait pas. L'énoncé demande de démontrer une équivalence '"si et seulement si". Essaie de rédiger de façon à répondre à ce cahier des charges.