bonjour, j'ai une fonction définie sur ]0;+infini[ par f(x)=e^x/x.
j'ai deux questions :
1) soit m un nombre réel. préciser, en fonction des valeurs du nombre réel m, le nombre de solutions de l'équation f(x)=m
2) on note delta la droite d'équation y=-x.
On note A un éventuel point de Cf d'abscisse a en lequel la tangente à la courbe Cf est parallèle à la droite delta.
a/ Montrez que a est solution de l'équation e^x(x-1)+x^2=0.
On note g la fonction définie sur [0;+infini[ par g(x)=e^x(x-1)+x^2
On admet que g est dérivable et on note g' sa dérivée.
b/ calculer g'(x) pour tout nombre réel x de l'intervalle [0;+infini[, puis dresser le tableau de variations de g sur [0;+infini[. (j'ai réussi cette question)
c/ montrez qu'il existe un unique point A en lequel la tangente à Cf est parallèle à la droite delta.
en résumé, j'ai besoin d'aide pour 1); 2a/ et 2c/
Merci à ceux qui prendrons le temps de m'aider !
Maths exponentielle
8 messages
- Page 1 sur 1
Re: maths exponentielle
2a. Deux droites parallèles ont même coefficient directeur.
2c. Qu'as-tu trouvé à la question 2b ?
2c. Qu'as-tu trouvé à la question 2b ?
Re: maths exponentielle
Sa Majesté a écrit:2a. Deux droites parallèles ont même coefficient directeur.
2c. Qu'as-tu trouvé à la question 2b ?
2b, je trouve e^x+e^x(x-1)+2x
Re: maths exponentielle
Bonjour,
1)
f(x)=e^x/x pour x > 0
f'(x) = e^x * (x-1)/x²
f('x) a le signe de (x-1) car ...
Etudier le signe de f'(x) et montrer que :
f'(x) < 0 pour x dans ]0 ; 1[ --> f est décroissante
f'(x) = 0 pour x = 1
f'(x) > 0 pour x > 1 --> f est décroissante
f est minimum pour x = 1
Calculer f(1) = e
calculer lim(x-->0+) f(x) = ...
calculer lim(x-->+oo) f(x) = ...
avec tout ce qui précède, un rien de réflexion donne le mombre de solutions de f(x) = m en fonction de la valeur de m
Pour m < e, il y a ... solution(s)
Pour m = e, il y a ... solution(s)
Pour m > e, il y a ... solution(s)

1)
f(x)=e^x/x pour x > 0
f'(x) = e^x * (x-1)/x²
f('x) a le signe de (x-1) car ...
Etudier le signe de f'(x) et montrer que :
f'(x) < 0 pour x dans ]0 ; 1[ --> f est décroissante
f'(x) = 0 pour x = 1
f'(x) > 0 pour x > 1 --> f est décroissante
f est minimum pour x = 1
Calculer f(1) = e
calculer lim(x-->0+) f(x) = ...
calculer lim(x-->+oo) f(x) = ...
avec tout ce qui précède, un rien de réflexion donne le mombre de solutions de f(x) = m en fonction de la valeur de m
Pour m < e, il y a ... solution(s)
Pour m = e, il y a ... solution(s)
Pour m > e, il y a ... solution(s)
Re: maths exponentielle
Black Jack a écrit:Bonjour,
1)
f(x)=e^x/x pour x > 0
f'(x) = e^x * (x-1)/x²
f('x) a le signe de (x-1) car ...
Etudier le signe de f'(x) et montrer que :
f'(x) < 0 pour x dans ]0 ; 1[ --> f est décroissante
f'(x) = 0 pour x = 1
f'(x) > 0 pour x > 1 --> f est décroissante
f est minimum pour x = 1
Calculer f(1) = e
calculer lim(x-->0+) f(x) = ...
calculer lim(x-->+oo) f(x) = ...
avec tout ce qui précède, un rien de réflexion donne le mombre de solutions de f(x) = m en fonction de la valeur de m
Pour m < e, il y a ... solution(s)
Pour m = e, il y a ... solution(s)
Pour m > e, il y a ... solution(s)
Merci beaucoup ! Donc si je comprends bien :
Pour m<e, il y a 2 solutions.
Pour m=e, il y a 1 solution.
Pour m>e, il y a 2 solutions.
Car c'est une parabole et la courbe y=x coupe 2 fois Cf ?
Re: maths exponentielle
Merci beaucoup ! Donc si je comprends bien :
Pour m<e, il y a 2 solutions.
Pour m=e, il y a 1 solution.
Pour m>e, il y a 2 solutions.
Car c'est une parabole et la courbe y=x coupe 2 fois Cf ?
Ce n'est pas une parabole ... même si le dessin de f(x) ressemble un peu à une parabole.
Et ta réponse "Pour m<e, il y a 2 solutions" est fausse.
Re: maths exponentielle
Black Jack a écrit:Merci beaucoup ! Donc si je comprends bien :
Pour m<e, il y a 2 solutions.
Pour m=e, il y a 1 solution.
Pour m>e, il y a 2 solutions.
Car c'est une parabole et la courbe y=x coupe 2 fois Cf ?
Ce n'est pas une parabole ... même si le dessin de f(x) ressemble un peu à une parabole.
Et ta réponse "Pour m<e, il y a 2 solutions" est fausse.
Oui, c'est vrai que la courbe y ressemble grandement. Alors pour m<e, il y a 1 solution ?
Re: maths exponentielle
noa a écrit:Black Jack a écrit:Merci beaucoup ! Donc si je comprends bien :
Pour m<e, il y a 2 solutions.
Pour m=e, il y a 1 solution.
Pour m>e, il y a 2 solutions.
Car c'est une parabole et la courbe y=x coupe 2 fois Cf ?
Ce n'est pas une parabole ... même si le dessin de f(x) ressemble un peu à une parabole.
Et ta réponse "Pour m<e, il y a 2 solutions" est fausse.
Oui, c'est vrai que la courbe y ressemble grandement. Alors pour m<e, il y a 1 solution ?
Ben non, c'est encore faux.
Il faut comprendre ce qu'on fait et pas lancer des réponses au hasard.
Pour comprendre "visuellement" :
On trace (sur une calculette graphique par exemple), le graphe de y = f(x), en choisissant judicieusement la plage représentée pour la variable x.
Et si on veut len ombre de solution à f(x) = m ... on trace sur le même graphe la droite d'équation y = m (avec m une valeur numérique choisie)...
Si je veux tester m < e, on peut par exemple prendre m = 2.
On trace donc le graphe de y = f(x) et celui de la droite d'équation y = 2 ... on obtient ceci :
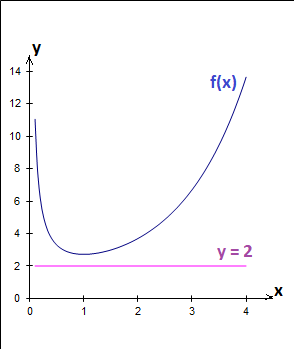
Le nombre de solution(s) de f(x) = m est le nombre de point(s) de rencontre de la courbe de f(x) et de la droite.
On voit que la droite ne rencontre pas le graphe de f(x) ... et donc il n'y a pas de solution.
Compris ?
Refais-le avec m = e et puis avec un m > e et regarde ce qui se passe pour le nombre de points de rencontre de la droite avec le graphe de y=f(x)
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 159 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
