Bonjour,
J'ai un dm de math pour lundi, et je n'arrive pas!!
J'espère que vous pourrez m'aider...Merci d'avance pour votre aide!
Enoncé:Les mathématiciens de la Grèce antique ont découvert et démontré l'irrationalité de racine carre de 2 à une époque qu'il est difficile de déterminer mais qu'on estime entre le 5eme et le 4eme siècle avant J-C. Dans cet exercice, on va prouver que racine carre de 2 n'est pas un nombre rationnel.
On rappelle qu'un nombre pair est un multiple de 2 et qu'un nombre impair n'est pas un multiple de 2.Un nombre pair peut donc toujours s'écrire sous la forme 2k et un nombre impair sous la forme 2k+1 où k est un nombre entier naturel.
1.a)Démontrer que si un nombre N est pair alors N² est pair.
b)Que peut on en déduire si N²est impair ?
c) Démontrer que si un nombre N est impair alors N²est impair.
d)Que peut on en déduire si N²est pair.
2.Pour démontrer que racine carre de 2 n'est pas un nombre rationnel, on va supposer qu'il l'est et montrer que l'on arrive alors à une absurdité.
Supposons qu'il existe deux nombre entiers naturels a et b#0 tels que racine carre de 2=a/b avec a/b irréductible.
a)Monter qu'alors on a: a²=2b².
b)Que peut on en déduire quant à la parité de a²? Et de a?
3.On admet donc que a est un nombre pair.
a)La fraction a/b étant irréductible, peut on avoir a et b tous les deux pairs ?
b)Que peut on en déduire quand à la parité de b ?
c)Montrer que a²est un multiple de 4.Que peut on en déduire pour b²?Quelle est donc la parité de b ?
4.Conclure.
Voilà!! C'est un peu long...
J'ai déjà effectue la question 1.
Je comprends vraiment pas.
Merci d'avance pour votre aide.
Dm de math
8 messages
- Page 1 sur 1
1.a)Démontrer que si un nombre  est pair alors
est pair alors 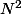 est pair.
est pair.
 est pair donc il existe
est pair donc il existe  tel que
tel que 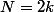 .
.
Du coup avec
avec  . Donc
. Donc 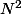 est pair
est pair
b)Que peut on en déduire si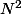 est impair ?
est impair ?
Si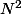 est impair, c'est qu'il n'est pas pair. On a donc la contraposée de ce qu'on vient de montrer en (1a).
est impair, c'est qu'il n'est pas pair. On a donc la contraposée de ce qu'on vient de montrer en (1a).
Cela signifie donc que dans ce cas est impair.
est impair.
c) Démontrer que si un nombre est impair alors
est impair alors 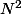 est impair.
est impair.
Même raisonnement qu'en (1a)
On pose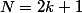 . Donc
. Donc  avec
avec 
d)Que peut on en déduire si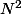 est pair.
est pair.
Que est pair (encore une fois la contraposée)
est pair (encore une fois la contraposée)
2.Pour démontrer que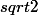 n'est pas un nombre rationnel, on va supposer qu'il l'est et montrer que l'on arrive alors à une absurdité.
n'est pas un nombre rationnel, on va supposer qu'il l'est et montrer que l'on arrive alors à une absurdité.
Supposons qu'il existe deux nombre entiers naturels et
et 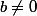 tels que
tels que  avec
avec 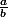 irréductible.
irréductible.
a)Monter qu'alors on a: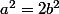 .
.
Là bien sûr c'est trivial...
b)Que peut on en déduire quant à la parité de ? Et de
? Et de  ?
?
On en déduit que est multiple de 2, donc pair. On a montré par ailleurs que si un carré est pair, le nombre de départ aussi (1d). Donc :
est multiple de 2, donc pair. On a montré par ailleurs que si un carré est pair, le nombre de départ aussi (1d). Donc :  EST PAIR
EST PAIR
3.On admet donc que est un nombre pair.
est un nombre pair.
a)La fraction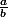 étant irréductible, peut on avoir
étant irréductible, peut on avoir  et
et  tous les deux pairs ?
tous les deux pairs ?
Clairement non, car si c'était le cas on pourrait simplifier par et donc la fraction ne serait pas irréductible (ce qu'on a supposé).
et donc la fraction ne serait pas irréductible (ce qu'on a supposé).
b)Que peut on en déduire quand à la parité de ?
?
Puisque est pair et que d'après (3a) les deux nombres ne peuvent pas être pairs en même temps,
est pair et que d'après (3a) les deux nombres ne peuvent pas être pairs en même temps,  EST FORCEMENT IMPAIR
EST FORCEMENT IMPAIR
c)Montrer que est un multiple de
est un multiple de  .Que peut on en déduire pour
.Que peut on en déduire pour  ?Quelle est donc la parité de
?Quelle est donc la parité de  ?
?
Comme est pair, il existe
est pair, il existe  tel que
tel que 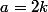 . Evidemment, on a alors
. Evidemment, on a alors 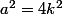 , c'est à dire que
, c'est à dire que  est multiple de
est multiple de  .
.
On a vu en (2a) que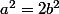 . Dans ce cas on a donc
. Dans ce cas on a donc  . Donc
. Donc  . Donc
. Donc  EST PAIR.
EST PAIR.
4.Conclure.
OUPS! En (3c) on trouve que est PAIR alors que en (3b) on trouve qu'il est IMPAIR.
est PAIR alors que en (3b) on trouve qu'il est IMPAIR.
IMPOSSIBLE!!!
DONC L'HYPOTHESE DE DEPART EST FAUSSE.
DONC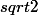 n'est pas rationnel.
n'est pas rationnel.
DONC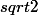 est irrationel.
est irrationel.
Du coup
b)Que peut on en déduire si
Si
Cela signifie donc que dans ce cas
c) Démontrer que si un nombre
Même raisonnement qu'en (1a)
On pose
d)Que peut on en déduire si
Que
2.Pour démontrer que
Supposons qu'il existe deux nombre entiers naturels
a)Monter qu'alors on a:
Là bien sûr c'est trivial...
b)Que peut on en déduire quant à la parité de
On en déduit que
3.On admet donc que
a)La fraction
Clairement non, car si c'était le cas on pourrait simplifier par
b)Que peut on en déduire quand à la parité de
Puisque
c)Montrer que
Comme
On a vu en (2a) que
4.Conclure.
OUPS! En (3c) on trouve que
IMPOSSIBLE!!!
DONC L'HYPOTHESE DE DEPART EST FAUSSE.
DONC
DONC
Grimmys a écrit:Il demandait de l'aide, non pas une soluce...
C'est vrai.
Mais entre-nous la présentation du problème est tellement machée, que la réponse était à 90% dans l'énoncé. Je veux dire par là que si la question avait été simplement "montrer que
Mais j'avoue que nous ne sommes pas là pour faire leurs devoirs. Cependant ce n'est pas forcément facile de trouver la bonne granularité d'aide.
Dans le cas présent, cela m'intéresserait de savoir pourquoi au juste il était bloqué. Je note d'ailleurs que nous n'avons pas encore de retour.
Laurent Watteau a écrit:Dans le cas présent, cela m'intéresserait de savoir pourquoi au juste il était bloqué.
si tu ne lui avais pas donné l'intégralité de la solution, tu saurais où il a bloqué. :hum:
par exemple, il ne sait pas que les nombres impairs sont de la forme 2k+1 et
que la réciproque est vraie, que 2k+1 est un nombre impair.
Il peut également ne pas savoir qu'une propriété ne peut pas être à la fois vraie et fausse.
Grimmys a écrit:Je pense qu'il aurait plutôt fallu lui demander des précisions : sur quel question exactement bloquait-il, et quel était le travail qu'il avait déjà produit...
c'est un doublon
http://www.maths-forum.com/dm-math-seconde-167807.php
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
