Logarithme népérien [Résolu]
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Benjigentil
- Membre Naturel
- Messages: 37
- Enregistré le: 10 Sep 2010, 18:51
-
 par Benjigentil » 30 Oct 2011, 14:43
par Benjigentil » 30 Oct 2011, 14:43
Bonjour,
J'ai vraiment du mal avec la fonction logarithme népérien.
On me donne
 = x^2 + 3x - xlnx)
et je dois donner l'ensemble de définition de cette fonction puis la dériver.
Mais j'ai du mal avec la rédaction. De plus c'est le
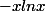
qui me bloque aussi ... !
Pourriez vous me donner des pistes de recherches ?
Merci beaucoup ! :mur:
-
vincentroumezy
- Membre Irrationnel
- Messages: 1363
- Enregistré le: 19 Juil 2010, 11:00
-
 par vincentroumezy » 30 Oct 2011, 14:58
par vincentroumezy » 30 Oct 2011, 14:58
Bonjour.
Tu sais que
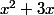
est défini sur

, mais que ln(x) est seulement définie sur....
Donc h(x) est seulement définie sur....
Pour dériver, tu sais dériver x²+3x, tu sais dériver x et ln(x), reste à utiliser la formule dedérivation d'un produit.
-
Benjigentil
- Membre Naturel
- Messages: 37
- Enregistré le: 10 Sep 2010, 18:51
-
 par Benjigentil » 30 Oct 2011, 19:53
par Benjigentil » 30 Oct 2011, 19:53
D'accord. Donc ma fonction est définie sur ] 0 ; + inf [ ?
Au niveau de la rédaction, comment dois-je justifier ?
Merci pour ton aide ! :lol3:
-
vincentroumezy
- Membre Irrationnel
- Messages: 1363
- Enregistré le: 19 Juil 2010, 11:00
-
 par vincentroumezy » 30 Oct 2011, 19:57
par vincentroumezy » 30 Oct 2011, 19:57
Oi, pour la rédaction ?
ln défini sur ]0;+l'infini[ donc h définie sur ]0;+l'infini[, puisque les autres fonctions élémentaires utilisées sont définies sur R.
-
Benjigentil
- Membre Naturel
- Messages: 37
- Enregistré le: 10 Sep 2010, 18:51
-
 par Benjigentil » 30 Oct 2011, 22:08
par Benjigentil » 30 Oct 2011, 22:08
Super merci beaucoup ! :lol3:
J'en profite pour un autre petit problème ( c'est le cas de le dire ).
La matière vivante retient dans ses tissus du carbone 14. Après la mort il se désintègre à raison de 1,2% tous les 100 ans. On note Un la quantité de carbone 14 contenue dans un échantillon après 100n années. Uo est donc la quantité de carbone 14 contenue dans l'échantillon initialement.
Je dois donner la nature de la suite et exprimer Un en fonction de n et Uo.
Selon moi Un = Uo - 0,012^n ... Mais ça ne colle pas pour la suite ... :triste:
Une aide ?
-
vincentroumezy
- Membre Irrationnel
- Messages: 1363
- Enregistré le: 19 Juil 2010, 11:00
-
 par vincentroumezy » 31 Oct 2011, 11:02
par vincentroumezy » 31 Oct 2011, 11:02
Petite erreur.
Après 100 ans, tu as perdu 1,2% de la quantité initiale, il te reste donc U1=U0-0,012*U0=U0(1-0,012)=0,988U0, etc....
-
Benjigentil
- Membre Naturel
- Messages: 37
- Enregistré le: 10 Sep 2010, 18:51
-
 par Benjigentil » 31 Oct 2011, 21:06
par Benjigentil » 31 Oct 2011, 21:06
D'accord !
Donc Un = Uo - 0,012*n ... C'est bien cela ? :we:
-
vincentroumezy
- Membre Irrationnel
- Messages: 1363
- Enregistré le: 19 Juil 2010, 11:00
-
 par vincentroumezy » 01 Nov 2011, 20:46
par vincentroumezy » 01 Nov 2011, 20:46
Non, Un=0,988^n*U0, on multiplie par 0,988 à chaque fois.
-
Benjigentil
- Membre Naturel
- Messages: 37
- Enregistré le: 10 Sep 2010, 18:51
-
 par Benjigentil » 01 Nov 2011, 23:00
par Benjigentil » 01 Nov 2011, 23:00
D'accord, j'ai compris merci beaucoup !
En revanche après je dois calculer au bout de combien d'année la quantité de carbone 14 aura diminué au moins de moitié !
Dois-je résoudre Uo*0,988^n
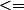
(Uo*0,988^n)/2 ??
-
vincentroumezy
- Membre Irrationnel
- Messages: 1363
- Enregistré le: 19 Juil 2010, 11:00
-
 par vincentroumezy » 02 Nov 2011, 09:25
par vincentroumezy » 02 Nov 2011, 09:25
Non, regarde ce que tu as écrit n'est jamais vrai !
On veut connaitre n tel que Un soit inférieur à la moitié de la quantité initiale de carbone 14.
-
Benjigentil
- Membre Naturel
- Messages: 37
- Enregistré le: 10 Sep 2010, 18:51
-
 par Benjigentil » 02 Nov 2011, 10:40
par Benjigentil » 02 Nov 2011, 10:40
Ah Oui ... :doh:
J'ai vraiment du mal ...
Donc je dois résoudre : 0,988^n*U0 < Uo/2 ?
J'espère que c'est juste cette fois ... ><'
-
Benjigentil
- Membre Naturel
- Messages: 37
- Enregistré le: 10 Sep 2010, 18:51
-
 par Benjigentil » 02 Nov 2011, 10:48
par Benjigentil » 02 Nov 2011, 10:48
Parce que je vois pas trop comment on peut faire sans avoir Uo ... ?
-
vincentroumezy
- Membre Irrationnel
- Messages: 1363
- Enregistré le: 19 Juil 2010, 11:00
-
 par vincentroumezy » 02 Nov 2011, 14:13
par vincentroumezy » 02 Nov 2011, 14:13
Ben on n'en a pas besoin, essaye de résoudre, tu verras.
-
Benjigentil
- Membre Naturel
- Messages: 37
- Enregistré le: 10 Sep 2010, 18:51
-
 par Benjigentil » 02 Nov 2011, 19:47
par Benjigentil » 02 Nov 2011, 19:47
o,988^n * Uo < (Uo/2)
n*ln 0,988 * Uo < ln(Uo/2)
n => (ln(Uo/2)) / ( ln 0,988 )
Je suis bloqué là ... Sans la valeur de Uo ... Je vois pas comment faire ... :mur:
-
Benjigentil
- Membre Naturel
- Messages: 37
- Enregistré le: 10 Sep 2010, 18:51
-
 par Benjigentil » 02 Nov 2011, 20:41
par Benjigentil » 02 Nov 2011, 20:41
Ah, je peux simplifier par 1/Uo peut être ... ? Je n'en suis pas sûr ... :hum:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 81 invités