Limites trigonométriques

[Hanaconda]

Bonsoir tout le monde,
J'ai un exo sur les limites des fontions trigonométriques et je galère à le résoudre.
Merci de bien vouloir me prêter un coup de main.
Voici les limites ( c'est à partir de la 6 ) :



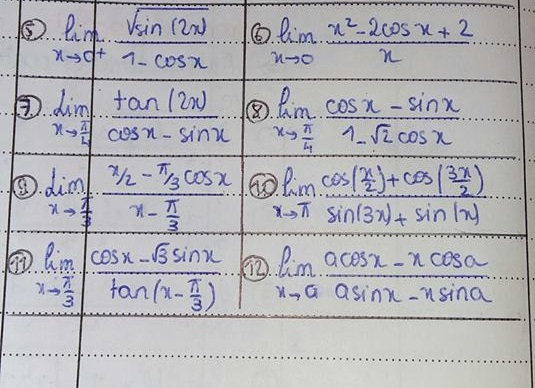
Bonne soirée!

[pascal16]

la 6 est faisable.
on peut écrire aussi : lim en 0 de (x+(2-2cos(x))/x)
(2-2cos(x))/x -> dérive le haut et le bas indépendamment, conclusion

a priori, quasiment toutes tes indéterminées se font comme ça, ton prof veut peut être faire apparaître exactement le nombre dérivé, il faut alors s'appliquer à faire du ((f(x)-f(a))/(x-a)) ou du (f(a+h)-f(a))/h.

pour les formes xxxx/(sin+cos), en multipliant par la quantité conjuguée, on a du yyyy/(sin²-cos²) qui lève l'indétermination.

[Hanaconda]

Merci de ton aide, mais je nj'ai pas vu le cours de la dérivation. Il veut que je les trouve en me servant des usuelles. Et jj'ai pu trouver la 5 et 6, c à partir de la 7 svp.

[pascal16]

pour la 7, tu peux transformer tan(2x) en 2sincos/(cos²-sin²), on se simplifie la vie en cherchant la limite de la fraction inverse.

la 8, sans dérivée, reste à poser x=pi/4 + t
on cherche alors la limite quand t tends vers 0.
on modifie par des équations trigo cos (pi/4+t)
j'ai pas fait les calculs, il reste peut-être une quantité conjuguée pour finir

...
la 10 -> vu la tête tu sais que tu dois d'abord soit doubler les angle en haut, soit couper en deux ceux du bas
...
la 12 -> c'est une simple quantité conjuguée valable du moment que a sina ne vaut pas 0.

[Hanaconda]

Merci beaucoup! Qu'en est-il des autres ( surtout la dernière..), svp?
Edit : C'est plutôt sin(2x)= 2sincos, le tan est différent, non?

[Hanaconda]

Je n'arrive pas à comprendre d'où vient le t, svp?

[pascal16]

si x = pi/4 +t
(c'est un décalage simple)

lim en pi/4 de f(x) = lim en 0 de f(t), démo :
|x-pi/4| < η ⇒ |f(x)-l| < ε
est équivalent à
|t| < η ⇒ |f(x)-l| < ε
car x-pi/4=t
et quand η devient aussi petit, t tend vers 0.
on a l'écriture de la limite de f(t) quand t tend vers 0

sinon, x =( x-pi/4) + pi/4
il faut tout développer
les cos et sin pi/4 se transforment en nombres
les parties en ( x-pi/4) tendent vers 0, on peut utiliser les compositions de limite connues
tu as deux fois plus de termes qui se simplifient ou pas.

[Hanaconda]

Je ne peux pas me servir d'une autre méthode? Je ne pense pas que je puisse procéder avec celle-là

[Hanaconda]

Pour la 7, je peux juste déviser le numé et le déno par x?

[Pseuda]

Bonjour,

Une idée pour la 8 : multiplie en haut et en bas par 1+V2 cos x (quantité conjuguée).

Pareil pour la 7 : multiplie en haut et en bas par cos(x)+sin(x) -> cela permet d'éliminer le cos(2x) en haut et en bas qui crée l'indétermination.

[Hanaconda]

Bonjour,
Je l'ai fait mais je suis tombée sur une forme indéterminée ( 0/0)

[Pseuda]

Bonjour,
Je l'ai fait mais je suis tombée sur une forme indéterminée ( 0/0)

Il faut continuer plus loin en factorisant en haut et en bas par cos(x)-sin(x) pour supprimer l'indétermination.
On a : 1-2 cos²(x)=sin²(x)-cos²(x)= ... ?

[Hanaconda]

comment se fait-il que 1-cos^2x soit egal à sin^2x - cos^2x svp?

[Pseuda]

comment se fait-il que 1-2*cos^2x soit egal à sin^2x - cos^2x svp?

C'est la base : 1=sin²(x)+cos²(x).

Donc 1-2cos²(x) = sin²(x)+cos²(x)-2cos²(x)= sin²(x)-cos²(x).

[pascal16]

c'est quand même bizarre que beaucoup de ces indéterminées sautent facilement avec la notion de nombre dérivé et qu'on ne travaille que des formules de trigo qui sortent du chapeau car il faut d'abord appliquer une ou plusieurs formules avant de savoir si elles marchent.

[Pseuda]

De mon côté, ce qui m'étonne, c'est que pour une fois, ils font les choses dans l'ordre : ils commencent par voir la notion de limite avant de voir la notion de dérivée (le contraire de ce qui est fait actuellement dans le programme du lycée).