Limites de suites
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
theluckyluke
- Membre Relatif
- Messages: 371
- Enregistré le: 01 Mai 2006, 10:13
-
 par theluckyluke » 01 Aoû 2006, 16:43
par theluckyluke » 01 Aoû 2006, 16:43
salut, je passe en Terminale S et je regarde un peu quleques points, et j'aurais voulu être éclairé pour deux trois petites choses...
Tout d'abord :
}{x})
j'ai procédé comme ceci :
}{x} = \lim_{x \to \0}\frac{sin(x) - sin(0)}{x-0} = \lim_{x \to \0}sin'(0) = \lim_{x \to \0}cos(0) = 1)
Est-ce que c'est juste?
Ensuite, les trois suivantes je bloque complétement :

, je ne sais pas comment faire avec cette racine.
Et enfin,

et
}{x})
Pourriez-vous m'aider?
Merci d'avance pour vos réponses.
+
 par metaphysiconigologien » 01 Aoû 2006, 17:23
par metaphysiconigologien » 01 Aoû 2006, 17:23
-Le raisonnement que tu fait pour trouver la lim de sinx/x en 0 est correct é c le moyen plus facile de le montrer. :id:
-Pour trouver la lim de sin(3x)/x il faut que tu pose X=3x é tu te sert de lim sinx/x en 0 = 0. normalement la limite de sin(3x)/x est 3.
- Puis pour les 2 autres limites tu multiplie le numérateur par son expréssion conjugué é l'indétermination est levé. pour la 1° limite c'est 1/4 é la 2° c'est 1/6. :zen:
Voila theluckyluke !!
-
Chimomo
- Membre Relatif
- Messages: 275
- Enregistré le: 17 Juin 2006, 09:23
-
 par Chimomo » 01 Aoû 2006, 17:41
par Chimomo » 01 Aoû 2006, 17:41
Tu pourras remarque que les limites 2 et 3 sont aussi des dérivées. 2 est la dérivée de f(x)= sqrt(x) en 4 et 3 est la dérivée de g(x)=sqrt(x+9) en 0.
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 01 Aoû 2006, 17:45
par Flodelarab » 01 Aoû 2006, 17:45
Il me semble bien que quand la fonction est continue et définie en un point, la limite est la valeur :ptdr:
limite de racine(x) quand x tend vers 4 égale 2
Considère la comme une valeur finie
pour l'avant dernière, factorise par racine (x)
et la der c de la trigo
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 02 Aoû 2006, 00:36
par Nightmare » 02 Aoû 2006, 00:36
Chimomo a écrit:Tu pourras remarque que les limites 2 et 3 sont aussi des dérivées. 2 est la dérivée de f(x)= sqrt(x) en 4 et 3 est la dérivée de g(x)=sqrt(x+9) en 0.
Ouch, les mathématiques en prennent un coup ... Que de rigueur ...
-
theluckyluke
- Membre Relatif
- Messages: 371
- Enregistré le: 01 Mai 2006, 10:13
-
 par theluckyluke » 02 Aoû 2006, 10:21
par theluckyluke » 02 Aoû 2006, 10:21
ok merci pour vos réponses...
pour tous j'ai compris, mais pour le sin(3x) je ne suis pas sûr alors je vais essayer de le faire et je vous donne ce que je trouve (si je trouve quelque chose bien-sûr)
-
Chimomo
- Membre Relatif
- Messages: 275
- Enregistré le: 17 Juin 2006, 09:23
-
 par Chimomo » 02 Aoû 2006, 11:15
par Chimomo » 02 Aoû 2006, 11:15
Désolé Nightmare mais quand je mettait 2 et 3 je faisais référence aux numéros des expressions, j'aurais effectivement du mettre une parenthèse.
Je ne faisais que donner une autre méthode pour parvenir au résultat (qui donne bien 1/4 et 1/6).
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 02 Aoû 2006, 12:51
par Nightmare » 02 Aoû 2006, 12:51
Ce n'était pas ce dont je parlais chimomo.
-
theluckyluke
- Membre Relatif
- Messages: 371
- Enregistré le: 01 Mai 2006, 10:13
-
 par theluckyluke » 02 Aoû 2006, 13:29
par theluckyluke » 02 Aoû 2006, 13:29
j'aurais encore besoin de votre aide pour celle-ci :
)
j'ai trouvé en multipliant par l'identité conjuguée
 (\sqrt{4x^2-5x+1} +2x))
ce qui donne

donc

c'est bon?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 02 Aoû 2006, 13:52
par Nightmare » 02 Aoû 2006, 13:52
Bonjour
Tu ne vois pas un petit problème ?
Tu multiplies par la quantité conjuguée, d'accord, mais il faut diviser par celle-ci en même temps sinon ça change ton expression.
-
Sdec25
- Membre Irrationnel
- Messages: 1002
- Enregistré le: 17 Juin 2006, 00:24
-
 par Sdec25 » 02 Aoû 2006, 13:55
par Sdec25 » 02 Aoû 2006, 13:55
Si tu multiplies par la quantité conjuquée il faut aussi diviser par la même quantité conjuquée.
(1-\frac{5}{4x}+\frac{1}{4x^2})}+2x})
Il reste plus qu'à faire quelques factorisations pour trouver la limite.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 02 Aoû 2006, 14:00
par Nightmare » 02 Aoû 2006, 14:00
Sinon sans même se compliquer la vie :
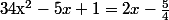^{2}-\frac{9}{16})
Par conséquent :
}}-2x)
La limite apparait tout de suite
:happy3:
-
Sdec25
- Membre Irrationnel
- Messages: 1002
- Enregistré le: 17 Juin 2006, 00:24
-
 par Sdec25 » 02 Aoû 2006, 14:13
par Sdec25 » 02 Aoû 2006, 14:13
T'as oublié un petit ² dans la racine :we:
Tu es sûr qu'on peut conclure tout de suite pour la limite ?
Car on ne peut pas dire que
} -1 \))
tend vers 0.
-
missoum
- Membre Naturel
- Messages: 39
- Enregistré le: 19 Juil 2006, 21:29
-
 par missoum » 02 Aoû 2006, 14:24
par missoum » 02 Aoû 2006, 14:24
Tout le monde n'a pas tes lunettes pour la voir Nightmare
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 03 Aoû 2006, 00:36
par Nightmare » 03 Aoû 2006, 00:36
Ce n'est pas une démonstration rigoureuse, mais on voit que la racine va tendre vers 1, donc intuitivement la limite va être celle de 2x-5/2-2x soit -5/2
:happy3:
-
theluckyluke
- Membre Relatif
- Messages: 371
- Enregistré le: 01 Mai 2006, 10:13
-
 par theluckyluke » 03 Aoû 2006, 09:26
par theluckyluke » 03 Aoû 2006, 09:26
ok, j'ai compris c'est bon...
oui effectivement j'ai fait une erreur un peu grossière...
merci
-
Sdec25
- Membre Irrationnel
- Messages: 1002
- Enregistré le: 17 Juin 2006, 00:24
-
 par Sdec25 » 03 Aoû 2006, 11:44
par Sdec25 » 03 Aoû 2006, 11:44
Nightmare a écrit:on voit que la racine va tendre vers 1, donc intuitivement la limite va être celle de 2x-5/2-2x soit -5/2
Je ne comprends pas bien car on a bien 2 équivalent de 2x mais on ne peut pas les soustraire.
Avec la même méthode on pourrait montrer que la limite est 0:

-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 03 Aoû 2006, 12:55
par Nightmare » 03 Aoû 2006, 12:55
j'avais bien dit que la méthode n'était pas rigoureuse :happy3:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 53 invités