Inverse de log décimal
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Dprime
- Membre Naturel
- Messages: 30
- Enregistré le: 19 Oct 2008, 19:00
-
 par Dprime » 18 Sep 2010, 16:17
par Dprime » 18 Sep 2010, 16:17
Bonjour,
J'aimerai savoir qu'elle est l'inverse de log. Je sais que par exemple, l'inverse de exp(x) est ln(x), ce qui donne dans une équation par ex:
24 = exp(2+x)
ln24 = 2+x
x= ln24 - 2
Mais pour:
24 = log(2+x)
Je ne sais pas comment faire, faut il utiliser log(x)=ln(x)/ln(10) ?
Ce qui ferait:
24 = ln(2+x)/ln10
24 x ln10 = ln(2+x)
exp(24 x ln10) = 2+x
x = exp(24 x ln10) -2
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 18 Sep 2010, 16:19
par Arnaud-29-31 » 18 Sep 2010, 16:19
Ce que l'on note ln est le logarithme en base e
Ce que l'on note log est le logarithme en base 10
Donc d'après toi ?
-
Dprime
- Membre Naturel
- Messages: 30
- Enregistré le: 19 Oct 2008, 19:00
-
 par Dprime » 18 Sep 2010, 16:23
par Dprime » 18 Sep 2010, 16:23
Si je reprend mon exemple c'est donc:
24 = log(2+x)
10 x 24 = 2+x
x = 240 -2 = 238
L'inverse de log est 10?
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 18 Sep 2010, 16:24
par Arnaud-29-31 » 18 Sep 2010, 16:24
Oui la fonction réciproque de log(x) est 10^x
La formule que tu utilises :
 = \frac{ln(x)}{ln(10)})
te donne la réponse.
En effet,
 = ln(10).log(x))
donc
} = e^{ln(10).log(x)})
Puis
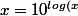})

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 18 Sep 2010, 16:26
par Ericovitchi » 18 Sep 2010, 16:26
24 = log(2+x)
10 x 24 = 2+x
attention pas 10 x 24 mais

-
Dprime
- Membre Naturel
- Messages: 30
- Enregistré le: 19 Oct 2008, 19:00
-
 par Dprime » 18 Sep 2010, 16:30
par Dprime » 18 Sep 2010, 16:30
Merci beaucoup, j'en avais besoin pour en exercice de chimie, sans ça, tout le reste était faux.
-
Dprime
- Membre Naturel
- Messages: 30
- Enregistré le: 19 Oct 2008, 19:00
-
 par Dprime » 18 Sep 2010, 16:31
par Dprime » 18 Sep 2010, 16:31
Merci Ericovitchi. :id:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
