Définition du log décimal
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
mimix
- Membre Naturel
- Messages: 74
- Enregistré le: 02 Nov 2010, 10:38
-
 par mimix » 03 Nov 2010, 11:21
par mimix » 03 Nov 2010, 11:21
Bonjour,
je bloque sur une définition du logarithme décimal. On a pn le nombre de chiffres de l'écriture de n en base 10. Et on me dit que si n s'écrit avec p chiffres, on a 10^(p-1) << n < 10^p. Ca vient de quelle définition du logdécimal?
merci à vous.
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 03 Nov 2010, 11:35
par arnaud32 » 03 Nov 2010, 11:35
 =ln(x)/ln(10))
ou si tu preferes
})
-
mimix
- Membre Naturel
- Messages: 74
- Enregistré le: 02 Nov 2010, 10:38
-
 par mimix » 03 Nov 2010, 11:41
par mimix » 03 Nov 2010, 11:41
Bonjour :),
comment faites-vous pour obtenir cette inégalité et pour faire apparaître p-1 et p en exposant?
merci.
-
mimix
- Membre Naturel
- Messages: 74
- Enregistré le: 02 Nov 2010, 10:38
-
 par mimix » 03 Nov 2010, 12:15
par mimix » 03 Nov 2010, 12:15
y a-t-il un lien entre les p-1, log etc?
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 03 Nov 2010, 12:26
par arnaud32 » 03 Nov 2010, 12:26
si p_n est le nombre de terme de n en base 10
tu as
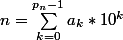
avec

et

tu en deduis quoi?
-
mimix
- Membre Naturel
- Messages: 74
- Enregistré le: 02 Nov 2010, 10:38
-
 par mimix » 03 Nov 2010, 12:40
par mimix » 03 Nov 2010, 12:40
Y a rien qui tilte.. :triste:
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 03 Nov 2010, 12:45
par arnaud32 » 03 Nov 2010, 12:45
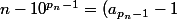*10^{p_n-1}+ \sum_{k=0}^{p_n-2}a_k*10^k)
avec

et

quels sont les signes des termes de droite? pkoi?
-
mimix
- Membre Naturel
- Messages: 74
- Enregistré le: 02 Nov 2010, 10:38
-
 par mimix » 03 Nov 2010, 12:53
par mimix » 03 Nov 2010, 12:53
Ils sont positifs, donc on a forcément n>> 10^pn-1
-
mimix
- Membre Naturel
- Messages: 74
- Enregistré le: 02 Nov 2010, 10:38
-
 par mimix » 03 Nov 2010, 12:55
par mimix » 03 Nov 2010, 12:55
ici on a des p à la place du pn, pourquoi?
Et pour l'autre inégalité, j'ai essayé de procédé pareil mais à droite je n'ai pas de termes négatifs, mais positifs
-
mimix
- Membre Naturel
- Messages: 74
- Enregistré le: 02 Nov 2010, 10:38
-
 par mimix » 03 Nov 2010, 13:29
par mimix » 03 Nov 2010, 13:29
Je ne vois toujours pas :s
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 03 Nov 2010, 13:35
par arnaud32 » 03 Nov 2010, 13:35
10^{p_n-1}=9*10^{p_n-1}+10^{p_n-1})
et
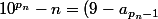*10^{p_n-1}+10^{p_n-1}-\sum_{k=0}^{p_n-2}a_k*10^k)
et ce te dis quoi ca?
-
mimix
- Membre Naturel
- Messages: 74
- Enregistré le: 02 Nov 2010, 10:38
-
 par mimix » 03 Nov 2010, 14:42
par mimix » 03 Nov 2010, 14:42
Désolé je ne vois pas où vous voulez en venir, enfin ce que vous voulez me faire dire plutôt.... ?
-
mimix
- Membre Naturel
- Messages: 74
- Enregistré le: 02 Nov 2010, 10:38
-
 par mimix » 03 Nov 2010, 23:24
par mimix » 03 Nov 2010, 23:24
En faîte c'est compris, j'm'étais trompé sur un signe.
merci!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 120 invités
