Salut !
Ok, le début ne me semble pas trop mal (après pour la question 1, tu mets "si ... alors" alors qu'en fait tu peux directement mettre des équivalences :
= g(x))
équivaut à (calculs) équivaut à
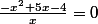
).

3. Tu cherches une primitive de la fonction
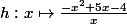
sur
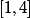
. Or on a montré que cette fonction était en fait la fonction
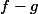
. Donc trouver une primitive de

revient à trouver une primitive de la différence de fonctions
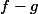
. Or une primitive d'une différence (ou somme) de fonction est égale à la différence (ou somme) des primitives de ces deux fonctions donc il suffit de trouver une primitive de

et

pour en déduire une primitive de

. En résumé, si je note abusivement par le symbole

pour signifier "une primitive de" alors je viens de dire que
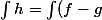 = \int f - \int g)
.
Attention, je te rappelle que prendre une primitive d'une fonction revient à effectuer le processus inverse lorsque tu dérives une fonction dans le sens où dire qu'une fonction

est une primitive d'une autre fonction f revient à dire que
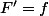
.
Par exemple, considérons la fonction
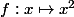
. Une primitive

de cette fonction est donnée par la fonction
=\frac 1 3 x^3)
. En effet, si tu dérives

, tu remarques qu'elle doit valoir

. Mais la primitive n'est pas unique, on aurait pu prendre par exemple
=\frac 1 3 x^3 +2\ 020)
, ou n'importe quelle autre constante additive puisqu'au final, en dérivant la constante devient nulle (mais en pratique on ne rajoute pas de constante additive, on la préfère nulle).
Entre autre, toute fonction admet
une unique dérivée alors que toute fonction admet
une infinité de primitives en ajoutant une constante additive quelconque. C'est pourquoi on parle de
la dérivée d'une fonction et d'
une primitive d'une fonction.
Dans l'exemple que j'ai pris précédemment :
-
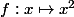
est la dérivée de la fonction
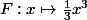
,
-
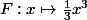
est une primitive de la fonction
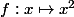
.
Comme pour les formules pour exprimées des dérivées de fonctions, je te laisse voir les formules pour calculer des primitives de fonctions. Normalement, tu dois trouver :
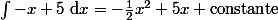
,
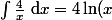+ {\rm constante})
.
4. Calculer l'aire de la partie colorée revient à calculer
\ {\rm d}x)
. En notant

une primitive de la fonction
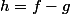
, tu auras alors directement que
\ {\rm d}x = H(4)-H(1)=...)
Je te laisse poursuivre