Integrale d'une fonction avec asymptote verticale
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Sephy
- Messages: 9
- Enregistré le: 13 Mar 2008, 18:29
-
 par Sephy » 07 Avr 2008, 10:10
par Sephy » 07 Avr 2008, 10:10
Bonjour, je me demandais s'il était possible de calculer l'intégrale suivante :

En effet, la fonction admet une asymptote verticale entre -1 et 1 (L'aire devient infinie au dessus et en dessous ? )
Les primitives de la fonction sont de la forme
=ln( \left|e^x+x\right|)+K)
avec K réel et

Donc ma question c'est est ce que
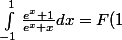-F(-1))
?
-
le_fabien
- Membre Complexe
- Messages: 2737
- Enregistré le: 05 Oct 2007, 10:00
-
 par le_fabien » 07 Avr 2008, 12:37
par le_fabien » 07 Avr 2008, 12:37
Et non on ne peut pas calculer cette integrale car la fonction n'est pas continue sur [-1;1]
-
Sephy
- Messages: 9
- Enregistré le: 13 Mar 2008, 18:29
-
 par Sephy » 07 Avr 2008, 12:46
par Sephy » 07 Avr 2008, 12:46
LEFAB11 a écrit:Et non on ne peut pas calculer cette integrale car la fonction n'est pas continue sur [-1;1]
Et je prouve comment la non-continuité de la fonction ? Je ne sais pas résoudre e^x + x = 0
-
le_fabien
- Membre Complexe
- Messages: 2737
- Enregistré le: 05 Oct 2007, 10:00
-
 par le_fabien » 07 Avr 2008, 12:53
par le_fabien » 07 Avr 2008, 12:53
Et bien tu poses f(x)=e^x+x
on a f'(x)=e^x+1>0 et d'après le théorème "de la bijection" tu montres que f s'annule une fois dans [-1;1]
-
Sephy
- Messages: 9
- Enregistré le: 13 Mar 2008, 18:29
-
 par Sephy » 07 Avr 2008, 13:26
par Sephy » 07 Avr 2008, 13:26
LEFAB11 a écrit:Et bien tu poses f(x)=e^x+x
on a f'(x)=e^x+1>0 et d'après le théorème "de la bijection" tu montres que f s'annule une fois dans [-1;1]
D'accord mais cela ne prouve pas la non-continuité ... Pour prouver une non continuité en a je montre que lim à gauche de a est different de lim à droite de a
-
le_fabien
- Membre Complexe
- Messages: 2737
- Enregistré le: 05 Oct 2007, 10:00
-
 par le_fabien » 07 Avr 2008, 13:32
par le_fabien » 07 Avr 2008, 13:32
f(x)=e^x+x s'annule sur [-1;1] pour une valeur xo (donc f(xo)=0)
alors limite (x tend vers xo) [(e^x+1)/f(x)]=infini
la fonction (e^x+1)/(e^x+x) n'est donc pas continue en xo
-
Sephy
- Messages: 9
- Enregistré le: 13 Mar 2008, 18:29
-
 par Sephy » 07 Avr 2008, 15:16
par Sephy » 07 Avr 2008, 15:16
LEFAB11 a écrit:f(x)=e^x+x s'annule sur [-1;1] pour une valeur xo (donc f(xo)=0)
alors limite (x tend vers xo) [(e^x+1)/f(x)]=infini
la fonction (e^x+1)/(e^x+x) n'est donc pas continue en xo
Merci bien :++:
-
Sephy
- Messages: 9
- Enregistré le: 13 Mar 2008, 18:29
-
 par Sephy » 07 Avr 2008, 15:37
par Sephy » 07 Avr 2008, 15:37
Y'a encore quelquechose qui me chiffone
LEFAB11 a écrit:Et non on ne peut pas calculer cette integrale car la fonction n'est pas continue sur [-1;1]
La justification n'est pas bonne, ce n'est pas parcequ'une fonction n'est pas continue qu'elle n'est pas intégrable. On peut bien intégrer E(x) sur n'importe quel segment non ?
-
le_fabien
- Membre Complexe
- Messages: 2737
- Enregistré le: 05 Oct 2007, 10:00
-
 par le_fabien » 07 Avr 2008, 19:09
par le_fabien » 07 Avr 2008, 19:09
Oui c'est vrai,il faut en plus une limite infinie en cette dicontinuité.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités