Asymptote verticale (limite)
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
saralecompte
- Membre Relatif
- Messages: 115
- Enregistré le: 19 Mar 2010, 14:47
-
 par saralecompte » 19 Mar 2010, 16:23
par saralecompte » 19 Mar 2010, 16:23
Salut tout le monde j suis en train de faire un devoir et j esite :s
j ai la fonction
x
f(x) = ----------
( x-1) au carré
et quand j veux faire la limite de x tendant vers 1 à gauche je ne sais pas si ca va donner 1/0- ou 1/0+ es ce que le carré va changer quelquechose?
Merci beaucoup
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 19 Mar 2010, 17:08
par Dinozzo13 » 19 Mar 2010, 17:08
Salut !
Pour tout

de
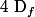
,
^2>0)
donc
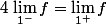
-
saralecompte
- Membre Relatif
- Messages: 115
- Enregistré le: 19 Mar 2010, 14:47
-
 par saralecompte » 19 Mar 2010, 17:23
par saralecompte » 19 Mar 2010, 17:23
merci beaucoup ca veux dire ke je n ai pas d asyptote vertical et donc pas de + ou - infini?
-
saralecompte
- Membre Relatif
- Messages: 115
- Enregistré le: 19 Mar 2010, 14:47
-
 par saralecompte » 19 Mar 2010, 17:26
par saralecompte » 19 Mar 2010, 17:26
mais j ai un autre probleme j continu mon exercice je dessine la fonction sur exel et j me rend compte k il y a des maximum et minimum mais quand je fais la derivé premiere j en trouve pas
[CENTER] x
f(x) = ----------
( x-1) au carré[/CENTER]
-
Teacher
- Membre Rationnel
- Messages: 732
- Enregistré le: 12 Nov 2007, 20:03
-
 par Teacher » 19 Mar 2010, 17:32
par Teacher » 19 Mar 2010, 17:32
Dis nous le résultat de f '(x) ?
-
saralecompte
- Membre Relatif
- Messages: 115
- Enregistré le: 19 Mar 2010, 14:47
-
 par saralecompte » 19 Mar 2010, 17:34
par saralecompte » 19 Mar 2010, 17:34
je trouve 3x² +2 / (x-1)^4
-
Teacher
- Membre Rationnel
- Messages: 732
- Enregistré le: 12 Nov 2007, 20:03
-
 par Teacher » 19 Mar 2010, 17:36
par Teacher » 19 Mar 2010, 17:36
C'est faux !
-
saralecompte
- Membre Relatif
- Messages: 115
- Enregistré le: 19 Mar 2010, 14:47
-
 par saralecompte » 19 Mar 2010, 17:39
par saralecompte » 19 Mar 2010, 17:39
j ai fait (u'v-uv')/v²
et pour avoir plus facile de dérivé le v' j ai dévelopé (x-1)² par x²-2x+2
en le dérivant je trouve 2x-2
-
Teacher
- Membre Rationnel
- Messages: 732
- Enregistré le: 12 Nov 2007, 20:03
-
 par Teacher » 19 Mar 2010, 17:41
par Teacher » 19 Mar 2010, 17:41
Donne moi u, v, u' ainsi que v'.
-
saralecompte
- Membre Relatif
- Messages: 115
- Enregistré le: 19 Mar 2010, 14:47
-
 par saralecompte » 19 Mar 2010, 17:49
par saralecompte » 19 Mar 2010, 17:49
(u/v)' = (u'v-uv')/v²
x'.(x²-2x+2)-x.(x²-2x+2)'/(x-1)^4
1.(x²-2x+2)-x.(2x-2)/(x-1)^4
x²-2x+2-2x²+2x/(x-1)^4
....
Haa voila en retapant mon calcul j ai vu ou j ai fai ma faute
donc je trouve normalement un max et un min en +-racine de 2
mais le probleme c est que ca ne corespond pas à mon ex-quation de depart :s
-
Teacher
- Membre Rationnel
- Messages: 732
- Enregistré le: 12 Nov 2007, 20:03
-
 par Teacher » 19 Mar 2010, 17:50
par Teacher » 19 Mar 2010, 17:50
Non !!! "(x-1)² par x²-2x+2" c'est faux !!!
(x-1)²=x²-2x+1² !! et 1²=1 !
-
saralecompte
- Membre Relatif
- Messages: 115
- Enregistré le: 19 Mar 2010, 14:47
-
 par saralecompte » 19 Mar 2010, 17:54
par saralecompte » 19 Mar 2010, 17:54
Donc normalement je devrai avoir un max en (1.42 ; 0.71) et un min en (-1.42 ; -2.43) et je n ai pas ca kan je dessine la fonction de depart sur excel
-
saralecompte
- Membre Relatif
- Messages: 115
- Enregistré le: 19 Mar 2010, 14:47
-
 par saralecompte » 19 Mar 2010, 17:55
par saralecompte » 19 Mar 2010, 17:55
ou lallalalala mon dieu je suis vraiment co***
j vai vite corrigé tout ca merci
-
saralecompte
- Membre Relatif
- Messages: 115
- Enregistré le: 19 Mar 2010, 14:47
-
 par saralecompte » 19 Mar 2010, 18:00
par saralecompte » 19 Mar 2010, 18:00
je trouve minimum en (-1; -0.25)
-
Teacher
- Membre Rationnel
- Messages: 732
- Enregistré le: 12 Nov 2007, 20:03
-
 par Teacher » 19 Mar 2010, 18:01
par Teacher » 19 Mar 2010, 18:01
C'est correct !
-
saralecompte
- Membre Relatif
- Messages: 115
- Enregistré le: 19 Mar 2010, 14:47
-
 par saralecompte » 19 Mar 2010, 18:09
par saralecompte » 19 Mar 2010, 18:09
merci :)
mais j ai toujours ce souci de ne pas trouvé ce min dans mon graphique sur excel :s
-
saralecompte
- Membre Relatif
- Messages: 115
- Enregistré le: 19 Mar 2010, 14:47
-
 par saralecompte » 19 Mar 2010, 18:11
par saralecompte » 19 Mar 2010, 18:11
merci
:happy2:
-
Teacher
- Membre Rationnel
- Messages: 732
- Enregistré le: 12 Nov 2007, 20:03
-
 par Teacher » 19 Mar 2010, 18:11
par Teacher » 19 Mar 2010, 18:11
Tu tapes la mauvaise fonction surement problème de parenthèses !

-
saralecompte
- Membre Relatif
- Messages: 115
- Enregistré le: 19 Mar 2010, 14:47
-
 par saralecompte » 19 Mar 2010, 18:16
par saralecompte » 19 Mar 2010, 18:16
c est correcte la cette dérivé?
((x-1)^4)' = (1-4).((x-1)^(4-1)).(x-1)' = -3.((x-1)^3).1
-
Teacher
- Membre Rationnel
- Messages: 732
- Enregistré le: 12 Nov 2007, 20:03
-
 par Teacher » 19 Mar 2010, 18:18
par Teacher » 19 Mar 2010, 18:18
non c'est faux

}^4}} \right]' = 4{(x - 1)^3})
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités

