[Exo ouvert] Integrale et somme convergente

par **Timothé Lefebvre** » 17 Aoû 2009, 14:38

Salut tout le monde !

A l'occasion de mes travaux sur le nombre pi, en preparation de mon TPE pour ceux qui s'en rappelle (voir mon post assez ancien dans le Cafe math.) je cherchais une somme sympathique a etudier et qui convergerait vers pi.
Je vous pose donc cet exo sous forme de 2 questions ouvertes, c'est a dire un enonce sans indications de methodes a suivre.

1) Calculer

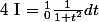
2) Soit

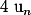
une suite avec

telle que

.
Prouver que cette suite converge et en determiner sa limite.

Bon courage

Tim

par **sky-mars** » 17 Aoû 2009, 14:49

Salut Tim
tu pense pas que la somme est un peu trop dur à justifier pour un niveau lycée ?
Tu balances une série numérique et pour justifier sa convergence on applique un théorème sur les séries alternées qu'on fait pas dans le secondaire

par **lapras** » 17 Aoû 2009, 14:51

C'est largement faisable sans ces outils !
c'est completement trivial que ca converge

par **sky-mars** » 17 Aoû 2009, 14:52

d'accord si vous le dites ... :space:

par **Timothé Lefebvre** » 17 Aoû 2009, 14:53

+1 lapras je l'ai fait sans outils du sup' ;)
Bon c'est sur il faut reflechir un peu, c'est le but du TPE que je vais presenter !

par **lapras** » 17 Aoû 2009, 14:53

Faut pas toujours penser aux gros outils ;) Ca peut etre handicapant.
(j'ai connu ca par exemple pour les inégalités aux olympiades)

par **ditans** » 17 Aoû 2009, 14:58

est ce qu'il faut utiliser un changement de variable pour l'intégrale? si oui ... ce n'est pas un niveau lycee, mais bon vu comme je suis douée au niveau des intégrales, doit y avoir autre chose

par **lapras** » 17 Aoû 2009, 14:59

ditans a écrit:est ce qu'il faut utiliser un changement de variable pour l'intégrale? si oui ... ce n'est pas un niveau lycee, mais bon vu comme je suis douée au niveau des intégrales, doit y avoir autre chose

Disons qu'il existe une primitive "connue".

par **sky-mars** » 17 Aoû 2009, 14:59

oui mais j'ai ce vieux réflexe de prendre l'outil le plus sophistiquée et de me faire les mouches avec le marteau pilon mdr
tu utilises les suites adjacentes alors ? en introduisant les termes paires et impaires ?

par **Timothé Lefebvre** » 17 Aoû 2009, 15:01

J'ai trouve de l'arctan la-dedans !
Sinon j'ai utilise une composee de fonctions puis le theoreme de derivation des composees ... Je ne dis plus rien !

par **sky-mars** » 17 Aoû 2009, 15:03

On parle de la série la ? mdr

par **Timothé Lefebvre** » 17 Aoû 2009, 15:04

Nan ^^ en post 10 je parlais de l'integrale.
Vers quoi converge la serie ?!

par **ditans** » 17 Aoû 2009, 15:06

lapras a écrit:Disons qu'il existe une primitive "connue".

ah oui "connue" car bon arctan on le voit pas ou rarement en terminale, ceci dit puisque c'est une primitive connue elle est faisable une fois qu'on connait la formule ... bref

par **sky-mars** » 17 Aoû 2009, 15:11

ta série converge vers

pardi !!

par **lapras** » 17 Aoû 2009, 15:14

Exact ! Mais il faut laisser chercher les lycéens !

par **sky-mars** » 17 Aoû 2009, 15:15

oui ils le chercheront j'ai donné aucune démonstration sa sera pas tombée du ciel comme je viens de le faire ^^ mdr

par **Timothé Lefebvre** » 17 Aoû 2009, 15:19

Ouais je trouve pareil ;)
Je suis nul en integrales aussi, ca m'a entraine !

par **busard_des_roseaux** » 17 Aoû 2009, 15:34

bonjour,

on peut calculer

par deux méthodes (de Term S ) et en déduire la valeur de

sans nommer la fonction réciproque arctan

par **egan** » 17 Aoû 2009, 16:54

Pour le 1, on pourrait créer une suite

telle que

, trouver une relation entre

et

.

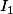
est facilement calculable donc ce serait finit. J'ai pas essayé par contre donc je sais pas trop si c'est faisable.

par **Timothé Lefebvre** » 17 Aoû 2009, 16:57

Ah oui j'avais pas pense a ca, j'ai bosse sur la derivee de la primitive F decoulant de l'integrale que j'ai compose avec une certaine fonction g que je ne vais pas donner :P

[Exo ouvert] Integrale et somme convergente

[Exo ouvert] Integrale et somme convergente

Qui est en ligne