Bonjour,
Je coince sur la série (j'ai pas réussi à faire marcher l'éditeur d'équation) :
"somme de n=0 jusqu'à l'infini de (3^n-1)/4^n"
Je dois trouver en quel valeur elle converge mais je n'ai aucune idée de la manière dont je dois procéder. Si quelqu'un pouvait m'aider, je lui serais reconnaissant.
Merci d'avance
URGENT : Somme d'une série convergente
8 messages
- Page 1 sur 1
Re: URGENT : Somme d'une série convergente
Bonjour
((3^n)-1)/4^n=((3/4)^n)-((1/4)^n)
Proposez un essai
Bon courage
((3^n)-1)/4^n=((3/4)^n)-((1/4)^n)
Proposez un essai
Bon courage
Re: URGENT : Somme d'une série convergente
Merci pour votre réponse,
J'ai toujours quelques difficultés. J'ai essayé de l'exprimer sous forme d'une série géométrique de la forme
ar^n-1 mais je me suis vite rendu compte que ce n'était pas possible. J'ai également essayé de faire la somme partielle des 8 premiers termes pour trouver une sorte de schéma qui se répeterait mais la suite est croissante puis décroissante et les résultats sont de plus en plus étranges.
J'ai toujours quelques difficultés. J'ai essayé de l'exprimer sous forme d'une série géométrique de la forme
ar^n-1 mais je me suis vite rendu compte que ce n'était pas possible. J'ai également essayé de faire la somme partielle des 8 premiers termes pour trouver une sorte de schéma qui se répeterait mais la suite est croissante puis décroissante et les résultats sont de plus en plus étranges.
Re: URGENT : Somme d'une série convergente
Il s'agit d'une différence de deux séries géométriques:
l'une de raison 3/4 et l'autre de raison 1/4.
Si vous y voyez plus clair ainsi, faites d'abord une somme de 0 à N,
scindez cette somme selon l'indication ci dessus, puis la conclusion n'est plus loin...
Continuez dans votre essai
PS (un détail) : au niveau lycée on n'étudie pas de série...n'est ce pas plutôt "supérieur " ?
l'une de raison 3/4 et l'autre de raison 1/4.
Si vous y voyez plus clair ainsi, faites d'abord une somme de 0 à N,
scindez cette somme selon l'indication ci dessus, puis la conclusion n'est plus loin...
Continuez dans votre essai
PS (un détail) : au niveau lycée on n'étudie pas de série...n'est ce pas plutôt "supérieur " ?
Re: URGENT : Somme d'une série convergente
Merci beaucoup,
Je me suis arrêté trop tôt dans ma réflexion
Et par rapport à mon niveau, je suis français et je vis actuellement au Canada, à Montréal. Je suis mes cours dans l'équivalent d'un lycée au Québec où le niveau dans les matières scientifiques est plus élevé qu'en France. Dans le système français, je devrais être en 1ère et je pensais que ces notions était abordé au niveau lycée, visiblement non .
.
Je me suis arrêté trop tôt dans ma réflexion
Et par rapport à mon niveau, je suis français et je vis actuellement au Canada, à Montréal. Je suis mes cours dans l'équivalent d'un lycée au Québec où le niveau dans les matières scientifiques est plus élevé qu'en France. Dans le système français, je devrais être en 1ère et je pensais que ces notions était abordé au niveau lycée, visiblement non
Re: URGENT : Somme d'une série convergente
OK
La question du niveau n'était qu'un détail de peu d'importance.
Il me semble qu'en France, au niveau première-terminale, on étudie la somme des termes de 0 à N,
mais sans se poser de question sur la limite (éventuelle) lorsque N tend vers +infini.
Revenez sur le forum si il y a encore une difficulté
Bon courage
La question du niveau n'était qu'un détail de peu d'importance.
Il me semble qu'en France, au niveau première-terminale, on étudie la somme des termes de 0 à N,
mais sans se poser de question sur la limite (éventuelle) lorsque N tend vers +infini.
Revenez sur le forum si il y a encore une difficulté
Bon courage
Re: URGENT : Somme d'une série convergente
Bonjour ,
il se pourrait qu'il manque des parenthèses et que le terme général de la série soit:
 que l'on peut écrire:
que l'on peut écrire:
}^n})
on a alors
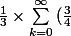^k=\frac{1}{3} \times \dfrac{1}{1-\frac{3}{4}}=\frac{4}{3})
il se pourrait qu'il manque des parenthèses et que le terme général de la série soit:
on a alors
Re: URGENT : Somme d'une série convergente
Re-bonjour
J'avais eu ce doute moi aussi,
mais finalement j'ai préféré répondre à l'énoncé tel qu'il était proposé.
Bref : IsaacMayras a à présent les deux lectures envisageables,
qu'il précise où sont ses parenthèses.
Bonne soirée à tous
J'avais eu ce doute moi aussi,
mais finalement j'ai préféré répondre à l'énoncé tel qu'il était proposé.
Bref : IsaacMayras a à présent les deux lectures envisageables,
qu'il précise où sont ses parenthèses.
Bonne soirée à tous
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
