Suite convergente : Classique

par **Rebelle_** » 30 Aoû 2010, 14:30

Nightmare a écrit:Benekire a bien intuité la définition : Un nombre est valeur d'adhérence d'une suite si n'importe quel intervalle centré en cette valeur contient une infinité de terme de la suite.

D'accord, je comprends bien ça, mais est-ce que le rayon dudit intervalle entre en ligne de compte ? Je suis sûre que oui parce que sinon ça ne sert à rien non ? Il faut que le rayon tende vers 0 non ? Enfin je m'exprime mal mais je crois que l'on note epsilon les très petites quantités.

par **benekire2** » 30 Aoû 2010, 14:30

Nightmare a écrit:Salut,

comment fais-tu déjà avec Bolzano-Weierstaß ? Même en l'utilisant, ce n'est pas trivial.

Non, même loin de l'être à vrai dire.

Et bien je considère

une extractrice telle que

soit convergente puisque u à le bon goût d'être bornée.
Je m'intéresse maintenant aux suites

En bidouillant avec l'égalité de départ je montre qu'elles ont des limites notées

et j'en déduit une expression explicite en fonction de k et je montre que

. Puis enfin, je montre rapidement que si une sous suite est bornée et que toute ses sous suites convergentes convergent vers un même réel alors cette suite converge vers ce même réel. J'applique ce résultat à l'exercice.

par **benekire2** » 30 Aoû 2010, 14:34

Rebelle_ a écrit:D'accord, je comprends bien ça, mais est-ce que le rayon dudit intervalle entre en ligne de compte ? Je suis sûre que oui parce que sinon ça ne sert à rien non ? Il faut que le rayon tende vers 0 non ? Enfin je m'exprime mal mais je crois que l'on note epsilon les très petites quantités.

Oui c'est ça, il faut qu'il reste une infinité de termes de la suite u dans un intervalle de la forme

pour tout

Dans ce cas là a est une VA.

par **Rebelle_** » 30 Aoû 2010, 14:36

Hum d'accord, je vois le principe. :)

par **Nightmare** » 30 Aoû 2010, 14:41

Ca me semble très compliqué mais ça à l'air de marcher. Ca me semble plus simple de considérer la récurrence

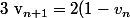avec

= notre valeur d'adhérence.

Pour une preuve niveau lycée, j'ai pas vraiment testé, mais une preuve ab absurdum en utilisant la définition de la limite ainsi qu'une petite récurrence me semble concluant.

par **benekire2** » 30 Aoû 2010, 14:43

Ouais, faut voir ... en tout cas elle ne peut pas diverger vers les infinis, c'est peut être à voir ... je vais écrire tout ça;

PS. Rebelle >> As-tu vu les définitions des limites de suite ?

par **Alpha** » 30 Aoû 2010, 14:45

Sauf erreur :

Déjà, on remarque que la suite constante Un = 2/3 fait l'affaire. En existe-t-il d'autres?

Supposons que ce soit le cas. Alors il existe n0 tel que U_n0 soit différent de 2/3. On aura donc U_n0 = 2/3 + a, avec a non nul.

Mais alors, U_(2n0) = 2(1-Un0) = 2 - 4/3 - 2a = 2/3 - 2a

et alors U_(4n0) = 2(1-U_2n0) = 2 - 4/3 - 4a = 2/3 + 4a....

Et ainsi de suite, U(n0*2^n) = 2/3 + (-1)^n * (2^n) * a.

On obtient donc que la suite n'est pas bornée, d'où on déduit que la seule suite qui convient est la suite constante égale à 2/3.

par **Rebelle_** » 30 Aoû 2010, 14:48

Ben j'ai vu ça en cours oui !

La définition donnait quelque chose comme : "Une suite converge vers l lorsque tout intervalle ouvert et centré sur l contient tous les termes de la suite à partir d'un certain rang".
Après j'ai vu ce que ça donnait graphiquement et puis la prof nous a écrit tout ça plus rigoureusement avec du langage mathématique (c'est de là que vient l'epsilon, je me rappelle de ce qu'elle avait noté).
Ensuite on a regardé des exemples (dont celui que tu as donné), et après on a vu comment montrer qu'une suite convergeait avec diverses méthodes.

Je crois que c'est à peu près tout sur les limites de suite.

par **benekire2** » 30 Aoû 2010, 14:50

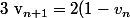Nightmare a écrit:Ca me semble très compliqué mais ça à l'air de marcher. Ca me semble plus simple de considérer la récurrence avec = notre valeur d'adhérence.

Euh, c'est un peu comme j'ai fait non ? C'est la même suite que j'utilise, j'ai peut être romancé le truc

par **Nightmare** » 30 Aoû 2010, 14:51

Salut,

On aura donc Un = 2/3 + a, avec a non nul.

C'est clairement faux, si U(n) n'est pas constamment égal à 2/3, elle peut être à peu près de toutes les formes qu'on veut !

N'importe quelle suite qui converge vers 2/3 vérifie l'énoncé, donc très peu de chance de montrer que les seules suite qui le vérifie sont constantes.

par **Nightmare** » 30 Aoû 2010, 14:52

benekire2 a écrit:Euh, c'est un peu comme j'ai fait non ? C'est la même suite que j'utilise, j'ai peut être romancé le truc

Ben, je sais pas, tu n'as pas démontré grand chose en même temps dans ton post :lol3: Cela dit, c'est effectivement la preuve "usuelle" que tout le monde a déjà vue, en tout cas, quand j'ai rencontré l'exo en sup, c'est la solution qu'on m'avait proposée.

par **benekire2** » 30 Aoû 2010, 14:53

Rebelle_ a écrit:Ben j'ai vu ça en cours oui !

La définition donnait quelque chose comme : "Une suite converge vers l lorsque tout intervalle ouvert et centré sur l contient tous les termes de la suite à partir d'un certain rang".
Après j'ai vu ce que ça donnait graphiquement et puis la prof nous a écrit tout ça plus rigoureusement avec du langage mathématique (c'est de là que vient l'epsilon, je me rappelle de ce qu'elle avait noté).
Ensuite on a regardé des exemples (dont celui que tu as donné), et après on a vu comment montrer qu'une suite convergeait avec diverses méthodes.

Je crois que c'est à peu près tout sur les limites de suite.

Mathématiquement ta définition équivaut à ;

Pour tout

il existe N tel que pour tout n,

Retiens les, elles sont assez importantes :id:

par **Alpha** » 30 Aoû 2010, 14:54

Nightmare a écrit:C'est clairement faux, si U(n) n'est pas constamment égal à 2/3, elle peut être à peu près de toutes les formes qu'on veut !

Non il s'agissait de mon U_n0, j'avais oublié l'indice 0, j'ai rectifié. Ce que j'ai écrit correspond donc à n'importe quelle suite non constante, puisque j'ai pris seulement un terme (celui de rang n0) différent de 2/3.

par **Rebelle_** » 30 Aoû 2010, 14:55

benekire2 a écrit:Mathématiquement ta définition équivaut à ;

Pour tout il existe N tel que pour tout n,

Retiens les, elles sont assez importantes :id:

Oui, c'est exactement ce qu'il y a dans mon cours ! Je viens d'ailleurs de le retrouver dans mon cahier

(heureusement que c'est toujours bien rangé).

par **benekire2** » 30 Aoû 2010, 14:58

Alpha a écrit:Non il s'agissait de mon U_n0, j'avais oublié l'indice 0, j'ai rectifié. Ce que j'ai écrit correspond donc à n'importe quelle suite non constante, puisque j'ai pris seulement un terme (celui de rang n0) différent de 2/3.

Oui mais une suite bornée convergent vers 2/3 n'est pas forcément constante.
Là où tu nous arnaque c'est quand tu écrit U_(2n0) = 2(1-Un0) , cela est faux,

par **Nightmare** » 30 Aoû 2010, 14:59

Alpha a écrit:Non il s'agissait de mon U_n0, j'avais oublié l'indice 0, j'ai rectifié. Ce que j'ai écrit correspond donc à n'importe quelle suite non constante, puisque j'ai pris seulement un terme (celui de rang n0) différent de 2/3.

Dans ce cas, c'est ok, mais n'aboutit pas. Le reste de mon message tient la route.

Exemple : u(n)=1/n+2/3 vérifie l'énoncé et n'est pas constamment égale à 2/3.

par **Alpha** » 30 Aoû 2010, 15:02

benekire2 a écrit:Là où tu nous arnaque c'est quand tu écrit U_(2n0) = 2(1-Un0) , cela est faux,

Mince, désolé, je me suis emmêlé les pinceaux!

Je sais pas pourquoi j'ai écrit ca sur ma feuille...

N'importe quelle suite qui converge vers 2/3 vérifie l'énoncé, donc très peu de chance de montrer que les seules suite qui le vérifie sont constantes.

Evidemment...

par **benekire2** » 30 Aoû 2010, 15:10

Pour la preuve lycée, où voit tu une récurrence ? On ne peut pas introduire notre suite de tout à l'heure puisque il nous faut Bolzano-Weirestrass ...

J'ai cherché avec les deux limites et essayé des les "faire communiquer" mais rien pour l'instant.

par **Finrod** » 30 Aoû 2010, 15:10

J'arrive à voir que si il existe un sous suite

bornée, k fixé, alors c'est bon.

En fait c'est même assez simple à voir, tout comme l'est le fait que ça sert à rien.

par **Nightmare** » 30 Aoû 2010, 15:13

Bon après m'être décidé à l'écrire, je confirme que la preuve que j'avais en tête niveau lycée (en connaissant la définition de la convergence) marche et n'est pas très compliquée.

Premiers pas : On procède par l'absurde : Ecrire la définition de la convergence de (u(n)+u(2n)/3) vers 1 et traduire en terme infinitésimaux le fait que u(n) ne converge pas vers 2/3. Essayer d'aboutir à une contradiction à l'aide de ces deux assertions.

Suite convergente : Classique

Qui est en ligne