Géométrie vectorielle

[jecomprendspas]

Voilà, c,est un problème que je bûche dessus depuis un bout et je n'y arrive pas plus. Seriez-vous capable de m'éclairer la-dessus?

Soit DROITE1:(x,y,z)= (2,2,5) + k(-1,2,-6) où k FAIT parti de R et PLAN1: -4x+4y-z=0 une droite et un plan dans R^3:

donnez l'équation vectorielle d'un plan PLAN2 contenant la droite DROITE1 et perpendiculaire au plan PLAN1;

[Razes]

Le vecteur est perpendiculaire au plan .
définis par le point et le vecteur
Le plan recherché est défini par le point et les vecteurs

[jecomprendspas]

merci Razes, donc la réponse serait PLAN2: (x,y,z)= (2,2,5) +k(-1,2,6) +s(-4,4,-1) ?

[Razes]

T'en ai pas sûr?

[jecomprendspas]

Sa fait du sens que vecteur naturel de D1 soit égal à un vecteur Directeur de plan2 vu que droite1 est perpendiculaire à plan1. C,est juste que sa sonne trop beau et simple pour être vrai. mais bon je te remerci grandement

[Razes]

Alors, c'est faux
Le vecteur est perpendiculaire au plan . Ce vecteur est tiré directement de l'équation du plan , on doit compléter ce vecteur avec un autre vecteur qui ne soit pas être parallèle au plan , c'est à dire qui ne soit pas perpendiculaire au vecteur 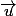. De plus la droite doit être comprise dans ce plan et d'autant plus son vecteur 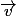fait l'affaire et le point aussi. Et le tour est joué.