Géométrie de R²

[h420]

Bonjour,

J'ai fais des exercices en TD mais je ne comprends toujours pas, malgré la correction de mon professeur.
L'exercice en question demande de représenter graphiquement différents ensembles.

Le premier ensemble à représenter est {(x,y) ∈ R² | y = x }
Pourriez vous m'expliquez le procédé pour que je puisse faire les autres question par moi même ?

Merci d'avance

[Mimosa]

Bonjour

Tu devrais reconnaitre l'équation d'une droite.

[mathelot]

Supposons le repère du plan orthonormé.
Ce sont les points à égale distance des axes x'Ox et y'Oy

[Sa Majesté]

Sujet déplacé dans la rubrique Lycée.
Ça ne peut pas être du Supérieur ... ou alors j'ai beaucoup vieilli !

[capitaine nuggets]

Salut !

Soit l'ensemble .
Dit autrement, est l'ensemble des points vérifiant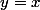, laquelle est l'équation d'une droite.
Tu peux aussi le voir comme ça : .

[chan79]

Supposons le repère du plan orthonormé.
Ce sont les points à égale distance des axes x'Ox et y'Oy

Pas tout-à-fait, je pense

[h420]

D'accord merci beaucoup, j'ai compris c'est tout bête. J'ai pu répondre aux questions suivantes mais je bloque à celle çi :

{(x,y) ∈ R² | y³-x ³ = 0 }

Je ne sais pas comment procéder pour faire la représentation graphique.

[mathelot]

ah oui, d'accord. je n'ai pas fait attention que cette définition (points à égale distance des axes x'Ox et y'Oy) englobe les points de la droite d'équation y=-x

[chan79]

D'accord merci beaucoup, j'ai compris c'est tout bête. J'ai pu répondre aux questions suivantes mais je bloque à celle çi :

{(x,y) ∈ R² | y³-x ³ = 0 }

Je ne sais pas comment procéder pour faire la représentation graphique.

salut

[aymanemaysae]

Bonjour;

L'indication de Chan79 te mène directement à la solution :

x³ - y³ = 0 ; donc : (x - y)(x² + yx + y²) = 0 ; donc : x - y = 0 ou x² + yx + y² = 0 .

Pour x - y = 0 : tu as déjà résolu ce cas .

Pour x² + yx + y² = 0 .
Si y = 0 , on a : x² = 0 ; donc : x = 0 ; donc le point (0 ; 0) est un élément de l'ensemble des solutions .
Si y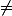 0 ; on a : x² + yx + y² = x² + 2 * (y/2) * x + (y/2)² - (y/2)² + y² = (x + y/2)² + 3/4 y² qui ne peut s'annuler pour tout y réel non nul .

On aurait pu remarquer que x² + yx + y² = 0 est une équation de second degré en x et chercher son discriminant en fonction de y qui est : Delta = y² - 4y² = -3y² qui est strictement négatif pour y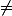 0 .